8 Unidad VI: Modelos lineales de poblaciones estructuradas
8.1 Proyección de matrices para modelos estructurados: la matriz de Leslie
Los modelos de poblaciones que hemos visto hasta la fecha sólo consideran un estado de desarrollo, tal que toda la población puede ser considerada como \(N\). Al hacer eso,incurrimos en una serie de supuestos biológicos muy fuertes, por ejemplo que todos los individuos nuevos en la población pueden reproducirse en cuanto se incorporan a esta con la misma probabilidad que los individuos más antiguos.
Parte de estos problemas biológicos que el modelo exponencial (\(N_{t+1} = \lambda N_t\)) en tiempo discreto presenta son solucionados por discretización de \(N\), es decir, dividir a \(N\) en una serie de compartimentos que representan estados de desarrollo, de modo que:
\[ N(t) = \left[\begin{array}{c} N_0(t)\\ N_1(t)\\ \vdots \\ N_n(t) \end{array}\right] \]
donde \(N_0(t)\) representa el cohorte más joven lo neonatos, y \(N_n(t)\) el de mayor edad. Los nacimiento entoces constituyen un flujo de invidiuos nuevos en la población hacia \(N_1(t)\), en función de los cohortes que se pueden reproducir. Para ejemplificar esto, consideremos un organismo cuyas dinámicas ocurren en tiempo discreto, con \(N\) dividido en cuatro edades\(N_0, N_1, N_2\) y \(N_3\). Consideremos primero cómo ocurre la transición entre estos compartimentos, donde sólo sobreviven 40% de \(N_0\) and \(N_1\), 30% de \(N_1\) a \(N_2\) y 10% de \(N_2\) and \(N_3\):
\[\begin{align} N_{1, t+1} &= 0.4 N_{0, t} \\ N_{2, t+1} &= 0.3 N_{1, t} \\ N_{3, t+1} &= 0.1 N_{2, t} \end{align}\]
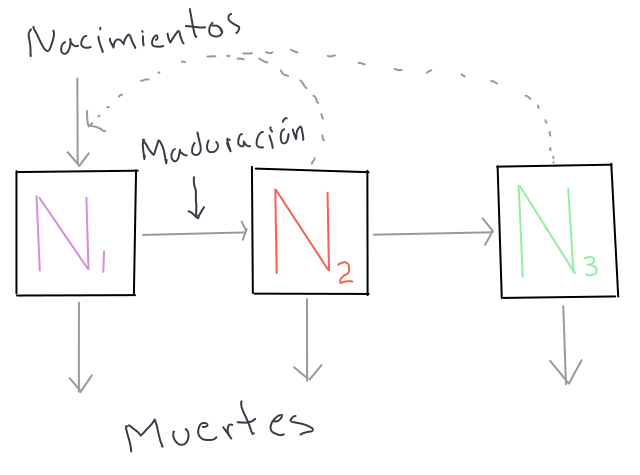
Figura 8.1: Diagrama del modelo de proyección de Matrices de Leslie con tres estadíos de desarrollo discretos. Las flechas sólidas representan flujo de individuos hacia y desde cada uno de los compartimentos que representa el número de individuos en cada categoría. Las flechas punteadas representan la fuente del flujo de individuos, por ejemplo los Nacimientos en N1 provienen de N2 y N3.
Para obtener \(N_0(t)\) necesitamos identificar los cohortes o compartimentos que sí se reproducen, entonces si estos son \(N_1\) y \(N_2\), la ecuación para \(N_0\) es:
\[\begin{align} N_{0, t+1} &= \mathrm{Crías\ nacidas\ de\ madres} N_{1, t} + \mathrm{Crías\ nacidas\ de\ madres} N_{2, t} \\ N_{0, t+1} &= 2 N_{1, t} + 1.5 N_{2, t} \end{align}\]
Claramente, en este modelo estamos asumiendo que la población de interés está constituida únicamente por hembras, de modo que \(2\) y \(1.5\) es el promedio de hembras nacidas por cada hembra en \(N_1\) y \(N_2\). Así tenemos entonces el modelo completo para representar como matriz:
\[\begin{equation} \left[\begin{array}{c} N_{0, t+1} \\ N_{1, t+1} \\ N_{2, t+1} \\ N_{3, t+1} \end{array}\right] = \left[ \begin{array}{cccc} 0 & 2 & 1.5 & 0 \\ 0.4 & 0 & 0 & 0 \\ 0 & 0.3& 0 & 0 \\ 0 & 0 & 0.1& 0 \end{array} \right] \tag{8.1} \end{equation}\]
La matriz de coeficientes en la ecuación (8.1) se conoce omo matriz de Leslie, y la notación corta para dichos sistemas de ecuaciones es:
\[\mathbf{N}(t+1) = L \mathbf{N}(t)\]
8.2 Análisis de los modelos de poblaciones estructuradas
8.2.1 Tablas de vida
Las tablas de vida son una herramienta estadística para organizar datos demográficos de fertilidad y supervivencia de las poblaciones. Existen algunas técnicas para generar tablas de vida, y una de las más confiables son los estudios de cohorte (conjunto de individuos que nacen en un período de tiempo específico, por ejemplo). En estos estudios, se lleva un registro cuidadoso de los sucesos de natalidad y mortalidad (8.1).
| Edad | No..Individuos | Muertes | Tasa |
|---|---|---|---|
| 0-0.5 | 1000 | 54 | 0.0540 |
| 0.5-1 | 946 | 145 | 0.1533 |
| 1-2 | 801 | 12 | 0.0150 |
| 2-3 | 789 | 13 | 0.0165 |
| 3-4 | 776 | 12 | 0.0155 |
| 4-5 | 764 | 30 | 0.0393 |
| 5-6 | 734 | 46 | 0.0627 |
| 6-7 | 688 | 48 | 0.0698 |
| 7-8 | 640 | 69 | 0.1078 |
| 8-9 | 571 | 132 | 0.2312 |
| 9-10 | 439 | 187 | 0.4260 |
| 10-11 | 252 | 156 | 0.6190 |
| 11-12 | 96 | 90 | 0.9375 |
| 12-13 | 6 | 3 | 0.5000 |
| 13-14 | 3 | 3 | 1.0000 |
Las tablas de vida entonces, enlistan el número de individuos y el rango de edades al inicio del estudio de cohorte, y el número de muertes que se presentaron mientras los individuos del cohorte se encontraban en cada rango de edades. Este tipo de arreglo permite estimar fácilmente las tasa de mortalidad, como en la tabla ??, donde la última columna, es el cociente de la 2a y 3a. Algunas tablas más complejas que la de Olaus Murie contienen una 5a y 6a columnas donde se reporta el número de crías totales y el cociente del número de individuos y crías para cada intervalo de edades.
Las tablas de vida han permitido describir algunas de las diferentes estrategias de los organismos con base en la probabilidad de morir en función de la edad (figura 8.2).
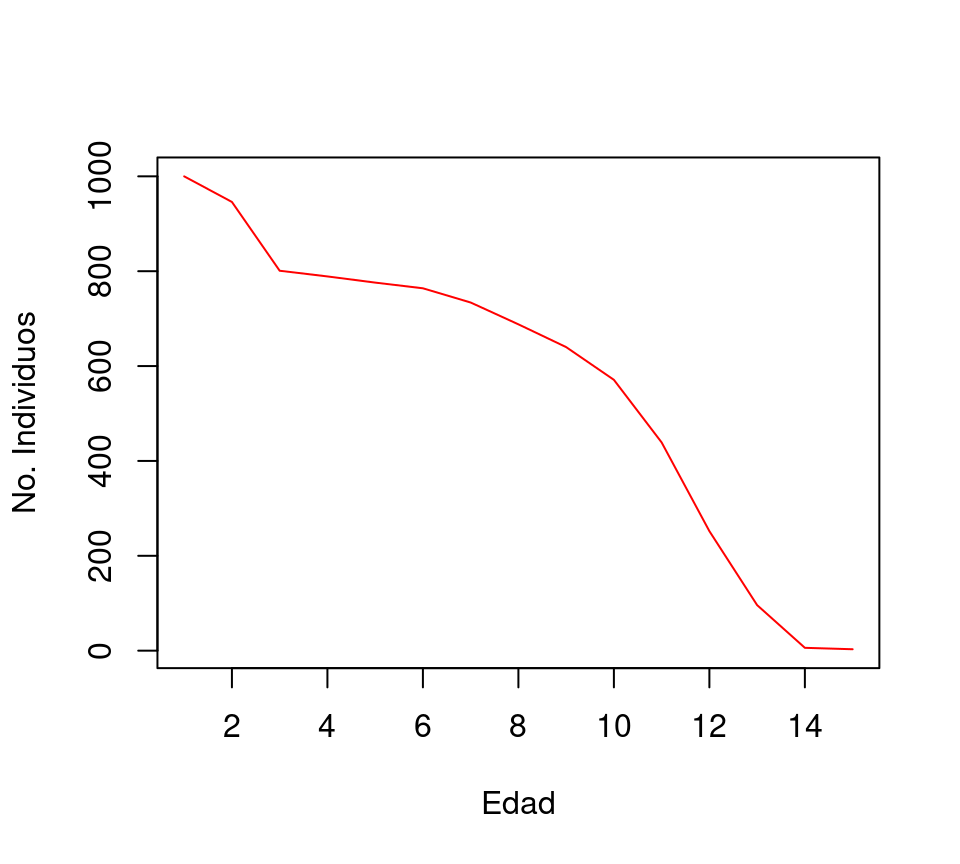
Figura 8.2: Rleación entre edad y supervivencia en Ovis dalli, de acuerdo con la tabla de vida del ejemplo.
La diversidad de estrategias reproductivas existentes resultan en curvas de supervivencia con otras formas. Por ejemplo la curva de Ovis dalli es convexa, lo cual quiere decir que la tasa de mortalidad aumenta con la edad. En plantas sin embargo, la curva es cóncava y quiere decir que las muertes ocurren mayoritariamente a edades tempranas, mientras que una pequeña fracción de individuos sobrevive a edades muy avanzadas.
Estras estrategias reproductivas también se manifiestan en la estructura de edades dentro de las poblaciones, es decir la cantidad de individuos neonatos, jóvenes y adultos que hay.
8.2.2 La ecuación de Euler
En demografía, se le conoce como la ecuación característica, y se utiliza para calcular la tasa neta reproductiva de una población. La interpretación del número producido por la ecuación a partir de los datos contenidos en una tabla de vida es el número de hembras con el que cada hembra es reemplazada, y este número se conoce como \(R_0\). Para calularlo necesitamos una tabla de vida para un cohorte de hembras, y hacer la suma:
\[\begin{equation} R_0 = \sum l_x m_x \tag{8.2} \end{equation}\]
donde \(l_x\) es la proporción viva del cohorte en cada categoría de edades (1 - columna 4 de tabla 8.1, o tasa de supervivencia por edad), y \(m_x\), el número promedio de descendientes hembras por cada hembra en cada categoría de edades \(x\).
Para dar un ejemplo utilizaremos otra tabla de vida para ardillas terrestres de Belding (Sherman and Morton 1984):
| Edad | l_x | m_x |
|---|---|---|
| 0 | 1.000 | 0.000 |
| 1 | 0.386 | 1.040 |
| 2 | 0.197 | 2.171 |
| 3 | 0.106 | 2.450 |
| 4 | 0.054 | 3.113 |
| 5 | 0.029 | 1.875 |
| 6 | 0.014 | 1.575 |
| 7 | 0.008 | 2.000 |
| 8 | 0.006 | 1.440 |
| 9 | 0.002 | 1.632 |
Como es evidente, nos queda por calcular \(l_x m_x\) que corresponde al producto de las 2a y 3a columnas. Una vez obtenido el producto podemos hacer la sumatoria, el código de R para hacer estas operaciones es:
lxmx <- tab2$l_x*tab2$m_x
sum(lxmx)## [1] 1.361258lo que indica que cada hembra en promedio será reemplazada por 1.36 hembras.
El concepto de \(R_0\) es también muy utilizado en epidemiología, donde tiene las mismas implicaciones. Si cada hembra es reemplazada en promedio por otra hembra (\(R_0 \approx 1\)), la población permanecerá estable, por el contrario si \(R_0 < 1\) la población tenderá a extinguirse. En epidemiología cada infectado deberá contagiar a más de uno para que haya una epidemia.
8.2.3 Valor reproductivo y autovectores
Las matrices de coeficientes de transición entre estados de desarrollo y las tasas de natalidad asociadas a cada estado pueden ser representadas con menos parámetros puesto que el crecimiento de la población continúa siendo exponencial. La manera de representar toda la matriz de coeficientes como uno sólo es con los valores propios. Veamos el ejemplo de la ecuación (8.1), cuyos valores propios son:
\[\lambda = \{0, 0.99, -0.24, -0.75 \}\]
Algunos de estos valores propios, como los negativos, son evidentemente, biológicamente insignificantes. En la práctica se elije sólamente uno de los valores propios, denominado valor dominante y que corresponde al valor más grande.
Como ya vimos en la unidad de álgebra de matrices, los valores propios también pueden ser números complejos, pero las implicaciones biológicas de estos valores propios no forman parte de esta unidad de modelos lineales.
8.3 Aplicaciones de lo modelo de matrices
Los modelos con matriz de Leslie tienen muchas aplicaciones en ecología, debido a que son sumamente flexibles y relativamente fáciles de implementar. Para comprender primero cómo funcionan y el tipode dinámicas que surgen con estos modelos echemos un vistazo al script de R