6 Unidad IV: Modelos deterministas basados en ecuaciones diferenciales ordinarias
6.1 Modelos lineales: Crecimiento exponencial (Malthusiano)
El modelo de crecimiento exponencial también recibe el nombre de “Malthusiano”, en honor al matemático inglés Thomas Malthus, quien acuñó la teoría demográfica subyacente en la publicación anónima de 1798 Ensayo sobre el principio de la población. Este libro trata, no de ecología, sino de las raíces de la pobreza en las sociedades capitalistas, según Malthus, ocasionada por la escasez de recursos. Muchas de las ideas de Malthus, son típicas del pensamiento colonial inglés del período en que vivió, sin embargo, son ecológicamente significativas.
El modelo malthusiano sugiere que, en ausencia de limitaciones, las poblaciones de humanos tenderían a crecer exponencialmente, de ahí que al modelo:
\[\begin{equation} \frac{dN}{dt} = rN \tag{6.1} \end{equation}\]
se le llame modelo de crecimiento malthusiano. La intepretación de \(r\) como la tasa de crecimiento sin limitación de alimento, espacio y en ausencia de competencia entre individuos o especies, es la principal aportación de Malthus, y ha servido de base para la formulación de teorías como la evolución.
6.1.1 Interpretación de \(r\)
Más que tasa de crecimiento, \(r\) representa la tasa de cambio del proceso que estamos observando. Estrictamente hablando una población cambia en razón a dos procesos, nacimientos y muertes. De manera relativamente obvia, los nacimientos representan el crecimiento de la población y las muertes del decrecimiento. Por lo tanto, es frecuente considerar que \(r = n - m\), con \(n=\) nacimientos y \(m=\) muertes. Si sustiuimos esta re-interpretación de \(r\), en la ecuación (6.1) tenemos:
\[\begin{equation} \frac{dN}{dt} = (n - m)N = nN - mN \end{equation}\]
esta re-parametrización del modelo es buena para ejemplificar que si \(n > m \rightarrow r>0\), si \(n < m \rightarrow r < 0\) y que si \(n = m \rightarrow r = 0\). El balance entre nacimientos y muertes entonces es la clave para que una población permanezca constante, crezca o disminuya.
Este balance entre nacimientos y muertes puede también ser concebido como flujos de entrada y salida de un compartimento (figura 6.1).
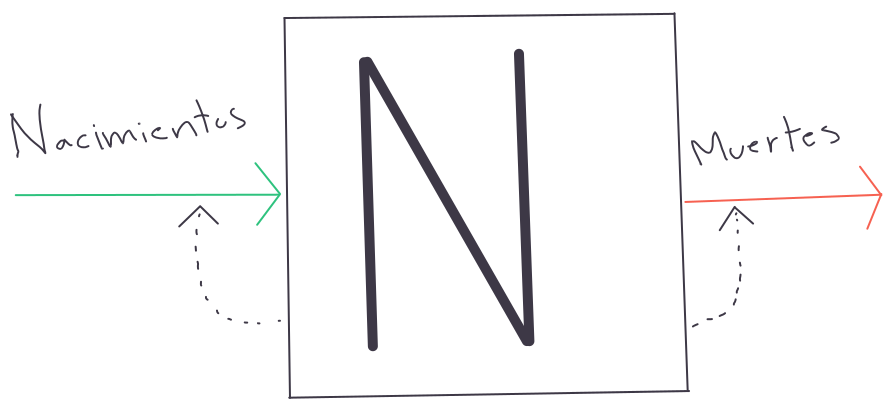
Figura 6.1: Esquema representativo del modelo de crecimiento malthusiano como flujo de nacimientos y muertes.
6.1.2 Análisis del modelo
Hasta el momento hemos visto ya muchas de las propiedades el modelo exponencial:
- Su derivada es equivalente al valor de la función misma
- Su antiderivada es por lo tanto, igualmente equivalente al valor de la función
- Puede ser representado, como ecuación diferencial, de manera implícita, sin que la variable independiente \(t\) aparezca en el lado derecho de la ecuación (6.1)
- Al ser representado de manera implícita, el modelo exponencial es lineal con respecto de la variable dependiente del tiempo
Estas propiedades hacen que analizar el modelo de crecimiento malthusiano sea relativamente sencillo.
6.1.3 Análisis de estabilidad
Este análisis surge de la pregunta ¿bajo qué condiciones una población \(N\) con tasa de crecimiento \(r\) permanece constante? Dada la ecuación (6.1) sabemos que si \(\frac{dN}{dt} > 0\), \(N \rightarrow \infty\), por el contrario si \(\frac{dN}{dt} < 0\), \(N \rightarrow 0\). Entonces, para que no haya cambios en \(N\), necesitamos que \(\frac{dN}{dt} = 0\). De esta equivalencia tenemos que si:
\[rN = 0\] Es debido a que, \(r=0\) si \(N \neq 0\), ó \(N=0\) si \(r \neq 0\). Es decir que el número de individuos \(N\) en una población permanecerá constante sólo bajo dos condiciones, si su tasa de crecimiento es cero, ó no tiene individuos.
6.1.4 Períodos de duplicación
Otra pregunta frecuente en el análisis de poblaciones es ¿cuánto tiempo tardará en duplicarse el tamaño de una población? Para responder esta pregunta, necesitamos la forma cerrada de la ecuación (6.1):
\[\begin{equation} N(t) = N_0 e^{rt} \tag{6.2} \end{equation}\]
En el análisis de estabilidad encontramos los casos en que \(\frac{dN}{dt} = 0\), por el contrario aquí nos interesa encontrar, con base en la ecuación (6.2) cuánto tiempo transcurrirá para que \(N(t) = 2N_0\), lo cual podemos conocer resolviendo:
\[2N_0 = N_0 e^{rt}\] para \(t\):
\[\begin{align} e^{rt} &= 2\\ \notag rt &= \ln 2\\ \notag t &= \frac{\ln 2}{r} \end{align}\]
Es así que podemos representar el período de duplicación de una población cualquiera como una función de su tasa de cambio (figura 6.2).
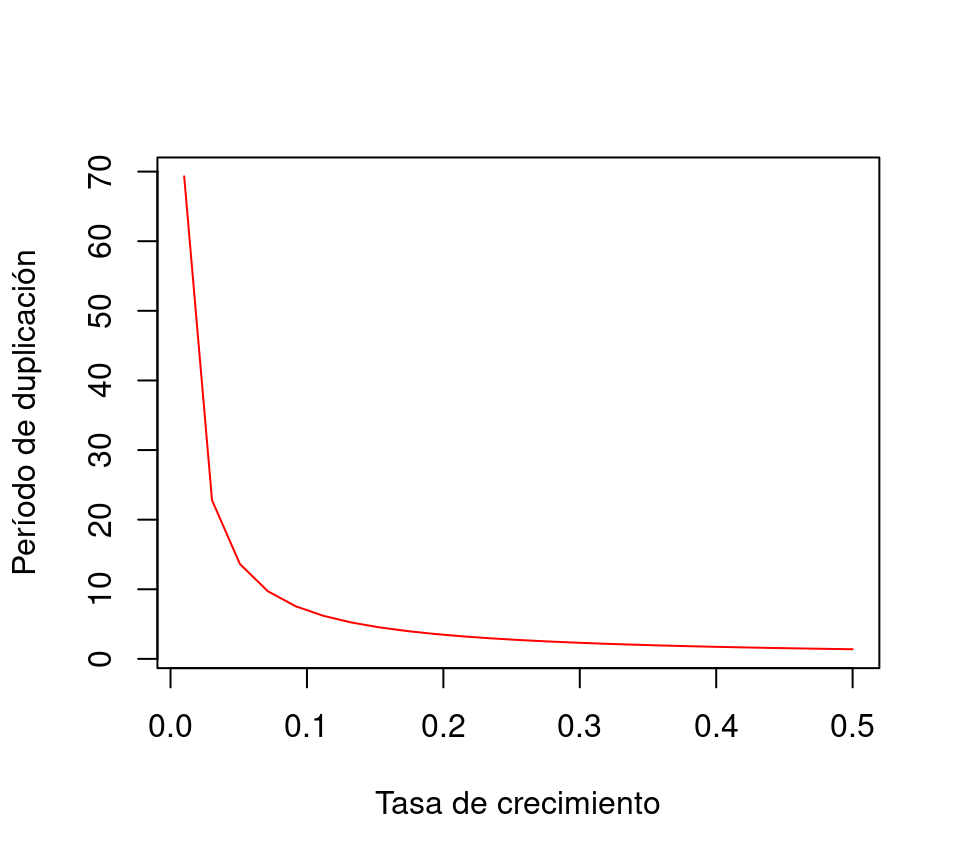
Figura 6.2: Período de duplicación en función de la tasa de crecimiento de una población.
6.1.5 Estimación de la tasa de cambio \(r\)
Para un ecólogo es de suma utilidad conocer la variación de \(r\) para poder medir los efectos del medio ambiente u otras especies sobre los cambios demográficos de una o varias poblaciones. En principio es posible obtener los posibles valores de \(r\) a partir de la ecuación (6.2), resolviéndola para \(r\):
\[\begin{align} \frac{N}{N_0} &= e^{rt}\\ \ln \left(\frac{N}{N_0} \right) &= rt\\ r &= \frac{\ln N - \ln N_0}{t} \end{align}\]
En caso de que tengamos observaciones puntuales de \(N\) y \(N_0\) a lo largo del tiempo.
6.1.6 Implicaciones del crecimiento exponencial
Una manera de visualizar las repercusiones el crecimiento exponencial y los períodos de duplicación queda de manifiesto con el acertijo:
Tenemos una población de bacterias que se duplica cada minuto, y tenemos cuatro frascos para albergarla. El primer frasco tardó una hora en llenarse, ¿cuánto tiempo pasará para que se llenen los tres frascos restantes?
6.2 Modelos no lineales: Crecimiento logístico de una población
Gracias a Thomas Malthus comprendimos qué sucede con una población cuando llega a estar libre de limitantes externas, sin embargo ¿cómo podemos representar lo que sucede con una población cuando existen dichas limitaciones? La respuesta es el modelo logístico. Este modelo es una variación del modelo malthusiano, pero para regular la tasa neta de crecimiento incorpora una segunda función de \(N\) que al multiplicar a \(r\) se vuelve cero cuando \(N\) alcanza un nivel definido como capacidad de carga (\(K\)).
El crecimiento logístico ocurre en el mundo real más frecuentemente que el malthusiano, pues todos los organismos vivientes crecen a expensas de otros, lo cual también se conoce como denso-dependencia, es decir, que el crecimiento neto de una población disminuye en relación a la cantidad de individuos.
La ecuación del modelo logístico es:
\[\begin{equation} \frac{dN}{dt} = rN \left(1 - \frac{N}{K} \right) \tag{6.3} \end{equation}\]
donde \(K\) es la capacidad de carga del área donde la población con \(N\) individuos vive. Como es evidente la expresión \((1-N/K) \rightarrow 0\) cuando \(N \rightarrow K\). De modo que una población con \(N < K\) tenderá a a crecer. Si expandimos \(rN(1 - N/K) = rN-rN^2/K\) podemos ver que se trata de una parábola. A diferencia del modelo de crecimiento exponencial, donde la tasa de cambio \(r\) es constante, en el modelo logístico, la tasa neta cambia con el tamaño de la población.
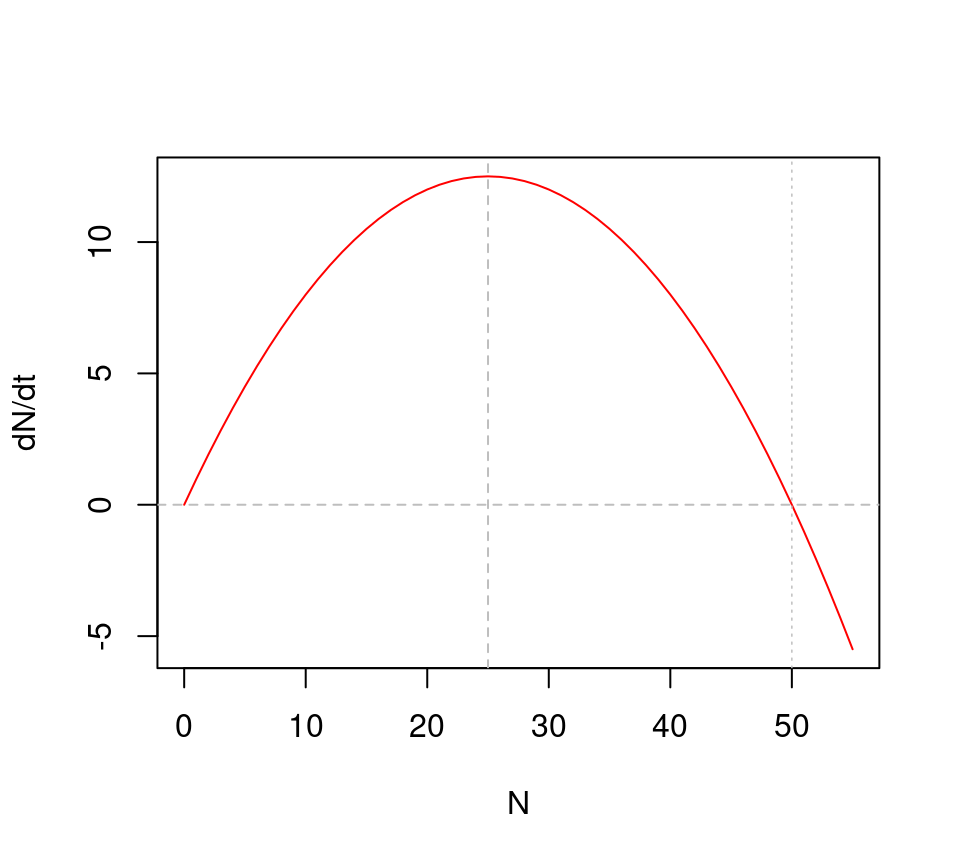
Figura 6.3: Tasa de cambio de N en relación a N en el modelo logístico, con K = 50 y r = 1
Algunas propiedades importantes del modelo logístico es que tiene una serie de puntos críticos. Por ejemplo, el tamaño de la población en que ingresa el número máximo de individuos nuevos, el cual corresponde a:
\[\begin{equation} \frac{d\left( \frac{dN}{dt} \right)}{dN} = r - 2rN/K = 0 \end{equation}\]
con lo que tenemos que:
\[ N= \frac{K}{2}\]
El crecimiento máximo se da cuando la población se encuentra al 50% de la capacidad de carga.
6.2.0.1 Análisis de estabilidad
Al igual que con el crecimiento malthusiano, nos interesa encontrar en qué situaciones la población será constante, por lo que tenemos que resolver:
\[\frac{dN}{dt} = 0\] para encontrar que hay dos puntos de equilibrio, \(N = 0\) y \(N = K\). Estos puntos tienen propiedades diferentes. Por ejemplo, ¿qué sucede con el \(N\) si a \(N=0\) le sumamos una cantidad muy pequeña \(\varepsilon\)? ¿\(N\) tenderá a regresar a \(0\)? Un ejemplo de este tipo de dinámicas en el mundo real se presenta con un péndulo, el cual tiene dos puntos de equilibrio, uno estable (donde el péndulo descansa en ausencia de una fuerza lateral), y otro inestable
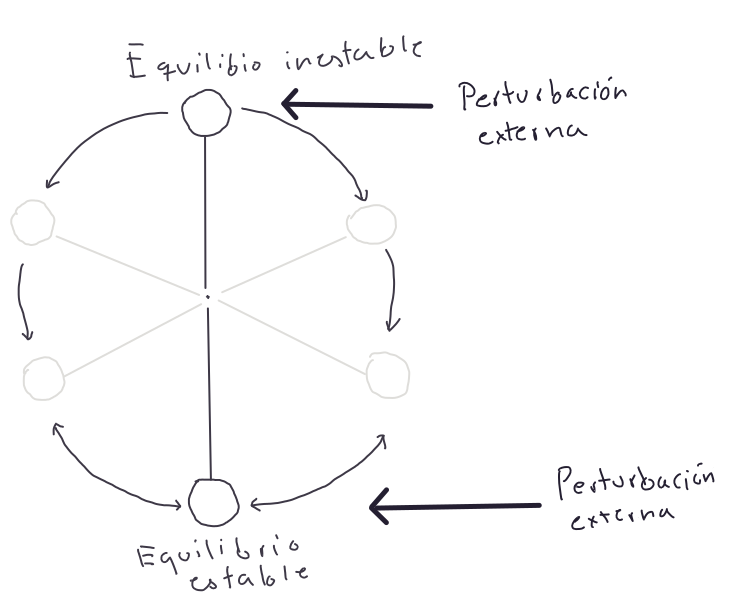
Figura 6.4: Puntos de equilibrio de un péndulo.
Las mismas preguntas aplican para \(N=K\). Para responderlas tenemos que hacer un paréntesis y echar un vistazo a la integración numérica.
6.2.0.1.1 Integración numérica
Esta técnica de integración está basada en la definición de la derivada como límite:
\[\begin{equation} f'(x) = \lim \limits_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \tag{6.4} \end{equation}\]
donde se asume que \(h = dx\), con \(dx \approx 0\), es decir, que \(dx\) es una cantidad arbitrariamente pequeña. De modo que sustituimos \(dx\) por \(h\) en (6.4) y resolvemos para \(f(x + dx)\) para obtener:
\[\begin{equation} f(x + dx) = f(x) + f'(x) \cdot dx \tag{6.5} \end{equation}\]
Este método es el más sencillo de los métodos numéricos de integración, y ha servido de punto de partida para el desarrollo de métodos más complejos y precisos.
Para integrar numéricamente el modelo logístico, utilizando la técnica de Euler (6.5), para lo que necesitamos conocer:
- \(r = 0.5\): la tasa neta de crecimiento poblacional
- \(K = 50\): la capacidad de carga poblacional
- \(N_0 = 1\): El tamaño inicial de la población
- \(dt = 1\): El tamaño de los incrementos de la variable independiente \(t\)
- \(t_{max}\): El tiempo máximo de simulación
Estos valores lo utilizaremos para conocer \(dN/dt\):
\[\frac{dN_0}{dt} = 0.5 \times N_0 \times \left (1 - \frac{N_0}{50} \right)=0.49\]
Por lo tanto \(N_1\) es:
\[N(1) = N_0 + \frac{dN_0}{dt} \times dt = 1 + 0.49 \times 1 = 1.49\] Este proceso se repite hasta que \(t = t_{max}\), y obtengamos \(N(t_{max})\). El código para integrar esta ecuación en R es:
#Parámetros
dt <- 1
r <- 0.5
K <- 50
# Variables
N <- numeric(25)
dN <- numeric(25)
# Valores iniciales
N[1] <- 1
dN[1] <- r*N[1] * (1 - N[1]/K)
# Integración
for(t in 2:25){
N[t] <- N[t-1] + dN[t-1] * dt
dN[t] <- r*N[t] * (1 - N[t]/K)
}
Figura 6.5: Simulación del modelo logístico con el método de Euler, con el código descrito aquí.
6.2.0.1.2 Análisis de estabilidad
Aquí veremos si los puntos de equilibrio \(N=0\) y \(N=K\) son estables o inestables. Para ello simularemos la ecuación con ambas condiciones iniciales, y les sumaremos una cantidad pequeña \(\varepsilon = 0.01\) para ver qué sucede con \(N\) en el resto de la simulación. En analogía con el péndulo, esperaríamos que \(N \rightarrow N^*\), el punto de equilibrio estable (\(0\) ó \(K\)) al aplicar la pertubación \(\varepsilon\) con ambas condiciones de inicio.
dt <- 1
r <- 0.5
K <- 50
# Variables
N <- numeric(25)
dN <- numeric(25)
E <- 0.01
# Valores iniciales
N[1] <- 0 + 0.01
dN[1] <- r*N[1] * (1 - N[1]/K)
# Integración
for(t in 2:25){
N[t] <- N[t-1] + dN[t-1] * dt
dN[t] <- r*N[t] * (1 - N[t]/K)
}
#Almacenamos el resultado con la condición inicial N=0+E en otro objeto N0
N0 <- N
#Repetimos para N=K+E
N <- numeric(25)
dN <- numeric(25)
N[1] <- K + 0.01
dN[1] <- r*N[1] * (1 - N[1]/K)
# Integración
for(t in 2:25){
N[t] <- N[t-1] + dN[t-1] * dt
dN[t] <- r*N[t] * (1 - N[t]/K)
}
NK <- N
Figura 6.6: Simulaciones para verificar tipo de puntos de equilibrio
6.3 Modelos en tiempo contínuo vs discreto
Todos los modelos que hemos visto en la presente unidad son dinámicos, representan procesos que cambian con el tiempo y su principal insumo son la condiciones presentes del sistema, las cuales determinan el estado futuro. Aprendimos a integrar ecuaciones diferenciales utilizando la definición de la derivada, y revirtiéndola asumiendo que \(h \approx dt\). Este proceso, es en esencia una discretización del tiempo, es decir, en lugar de evaluar \(f(t)\) para todos los puntos \(t\) posibles, lo aproximamos para intervalos separados por \(dt\). Por lo tanto las ecuaciones diferenciales integradas con métodos numéricos tienen algunas similitudes con los modelos en tiempo discreto:
Los modelos en tiempo discreto se conocen como ecuaciones en diferencias finitas, en comparación con las ecuaciones diferenciales que representan el tiempo de manera contínua.
La difefencia entre estos modelos consiste en los tiempos en que ocurren los eventos que representan. En los modelos de crecimiento poblacional los eventos representan la incorporación de invidiuos nuevos a la población. Por lo tanto, en un modelo de crecimiento contínuo los individuos nuevos entrar a la población “todo el tiempo”.
6.3.1 Crecimiento exponencial en tiempo discreto
Las ecuaciones de los modelos contínuo y discreto corresponden a:
\[\begin{align} \frac{dN}{dt} & = rN \tag{6.6} \\ N_{t+1} & = \lambda N \tag{6.7} \end{align}\]
donde las tasas de cambio son \(r\) y \(\lambda\). En el caso del modelo en tiempo discreto (6.7), se utiliza el parámetro \(\lambda\), puesto que \(\lambda = e^r\)
El crecimiento discreto tiene sentido biológico cuando los nacimientos de las poblaciones de algún organismo se sincronizan en un período de tiempo muy corto. El crecimiento exponencial contínuo, en contraste, representa las dinámicas de organismos que pueden reproducirse en cualquier momento. En un modelo de crecimiento discreto, los individuos nuevos entran a la población solamente en un momento preciso. La cantidad de individuos que ingresa a la pobalación al final de cada intervalo es la misma que en un modelo en tiempo contínuo (Figura 6.7). Por lo tanto, la selección de modelo tiene que estar informada por la biología del problema.
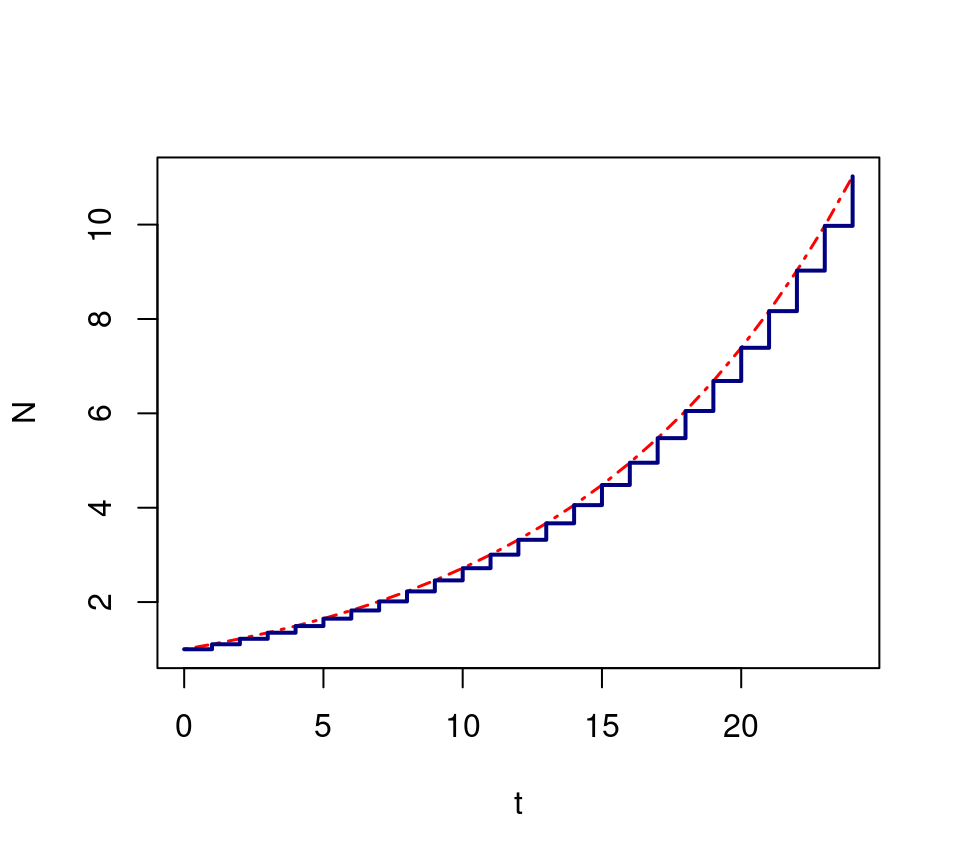
Figura 6.7: Diferencia entre modelos en tiempo contínuo (línea discontínua roja) y discreto (escalones en azul).
La escala exponencial del parámetro \(\lambda\) hace que la solución sea exacta, en comparación con la aproximación numérica con la ecuación de Euler del modelo en tiempo contínuo.
6.3.2 Crecimiento logístico en tiempo discreto
El modelo discreto es:
\[\begin{equation} N_{t+1} = \lambda N \left (1 - \frac{N}{K} \right) \end{equation}\]
en este caso \(\lambda\) está en la misma escala que en la ecuación (6.7). Como ya vimos anteriormente, esta versión del modelo de crecimiento logístico, tiene una serie de propiedades distintas al modelo contínuo, por lo que nos enfocaremos en este aspecto. Para ello, transformaremos sustuiremos \(N\) por \(x_t = N_t/K\), para analizar el tamaño de \(N\) en relación a la capacidad de carga:
\[\begin{equation} x_{t+1} = b(1-x_t)x_t \tag{6.8} \end{equation}\]
El análisis del comportamiento del modelo logístico es más fácil si se hace gráficamente, en especial porque puede ser complejo, porque puede ser caótico (Figura 6.8)

Figura 6.8: Ejemplos del comportamiento dinámico del modelo de crecimiento logístico, para tres valores de la tasa de crecimiento. En las figuras de la izquiera se muestra la correspondencia entre el tamaño de la población en t y el tamaño en t+1.
6.3.2.1 Implicaciones para sistemas ecológicos
Las dinámicas producidas por el sencillísimo modelo logístico en tiempo discreto sugieren que un sistema ecológico con esas características bien podría tener un comportamiento caótico. Como ecólogos es preciso preguntarnos si sólo se trata de artefactos matemáticos producto de la simplificación, o si en posible su ocurrencia. Modelos más complejos que toman en cuenta la existencia de diferentes sexos, por ejemplo, tienen un comportamiento más estable que los modelos sin esas estructuras Scheuring (2002).
La diferencia esencial entre el caos producido por el modelo logístico y el comportamiento errático de muchos sistemas ecológicos está en que el caos forma parte del funcionamiento del sistema, es determinístico, mientras que las variaciones de un sistema ecológico generalmente se consideran como fuerzas externas que cambian con el tiempo y que afectan al sistema.