7 Unidad V: Introducción al álgebra de matrices
7.1 Sistemas lineales
Un sistema lineal es un conjunto de ecuaciones lineales donde hay, idealmente, tantas variables como ecuaciones y viceversa. Cuando esta condición se cumple, se dice que el sistema está completo. La contraparte de estos sistemas son incompletos, y pueden tener más variables que ecuaciones ó más ecuaciones que variables.
Un sistema completo de ecuaciones lineales con dos variables sería:
\[2x + 3y = 4\]
\[4x - 2y =10\] Generalizando tenemos que un cualquier sistema lineal puede ser:
\[\begin{align} a_{1,1}x_1+a_{2,1}x_2 + \dots + a_{n,1}x_n & = b_1\\ a_{1,2}x_1+a_{2,2}x_2 + \dots + a_{n,2}x_n & = b_2\\ \vdots & \\ a_{1, n}x_1+a_{2,n}x_2 + \dots + a_{n,n}x_n & = b_n \end{align}\]
Cuando nos enfrentamos a un sistema como estos, la meta es encontrar los valores de \(x_1, x_2, \dots , x_3\) que satisfacen las igualdades. Para sistemas de dos ecuaciones, es fácil econtrar la solución utilizando una variedad de métodos, el primero de ellos, por graficación.
7.1.1 Solución gráfica
La solución para el sistema de ecuaciones del primer ejemplo:
\[\begin{align} 2x + 3y & = 4\\ 4x - 2y & =10 \end{align}\]
sería:

Figura 7.1: Solución gráfica del sistema de ecuaciones para dos variables
7.1.2 Solución algebráica
El método más sencillo en esta ocasión sería resolver la ecuación 2 para \(y\), pues la podemos simplificar dividiendo ambos lados entre 2:
\[ (4x - 2y)/2 = (10)/2 \rightarrow 2x - y = 5\] de donde obtenemos que:
\[y = 2x-5\]
Este valor de \(y\) en térmonos de \(x\), lo podemos sustituir en, la ecuación 1:
\[2x+3(2x-5) = 4\]
y resolvemos para \(x\) para obtener:
\[8x = 19 \rightarrow x = 19/8=2.375\]
Y entonces sustituimos a \(x\) en:
\(y = 2(2.375) - 5 = -0.25\)
Como se puede apreciar, resolver simples ecuaciones lineales puede ser laborioso. Es por ello que se desarrolló el álgebra de matrices, para resolver de eficientemente, sistemas de ecuaciones lineales con muchas variables. En esta unidad revisaremos brevemente los conceptos y técnicas más importantes del álgebra de matrices.
7.1.3 Sistemas lineales sin solución
En ocasiones, aunque un sistema de ecuaciones sea aparentemente completo, puede no tener solución. Por ejemplo el sistema:
\[\begin{align} x + y & = 1 \\ 2x + 2y & = 4 \end{align}\]
no tiene solución, lo cual se manifiesta gráficamente como dos líneas paralelas. Esto quiere decir que no existe un par de valores \(x\) y \(y\) que satisfagan las ecuaciones del sistema.
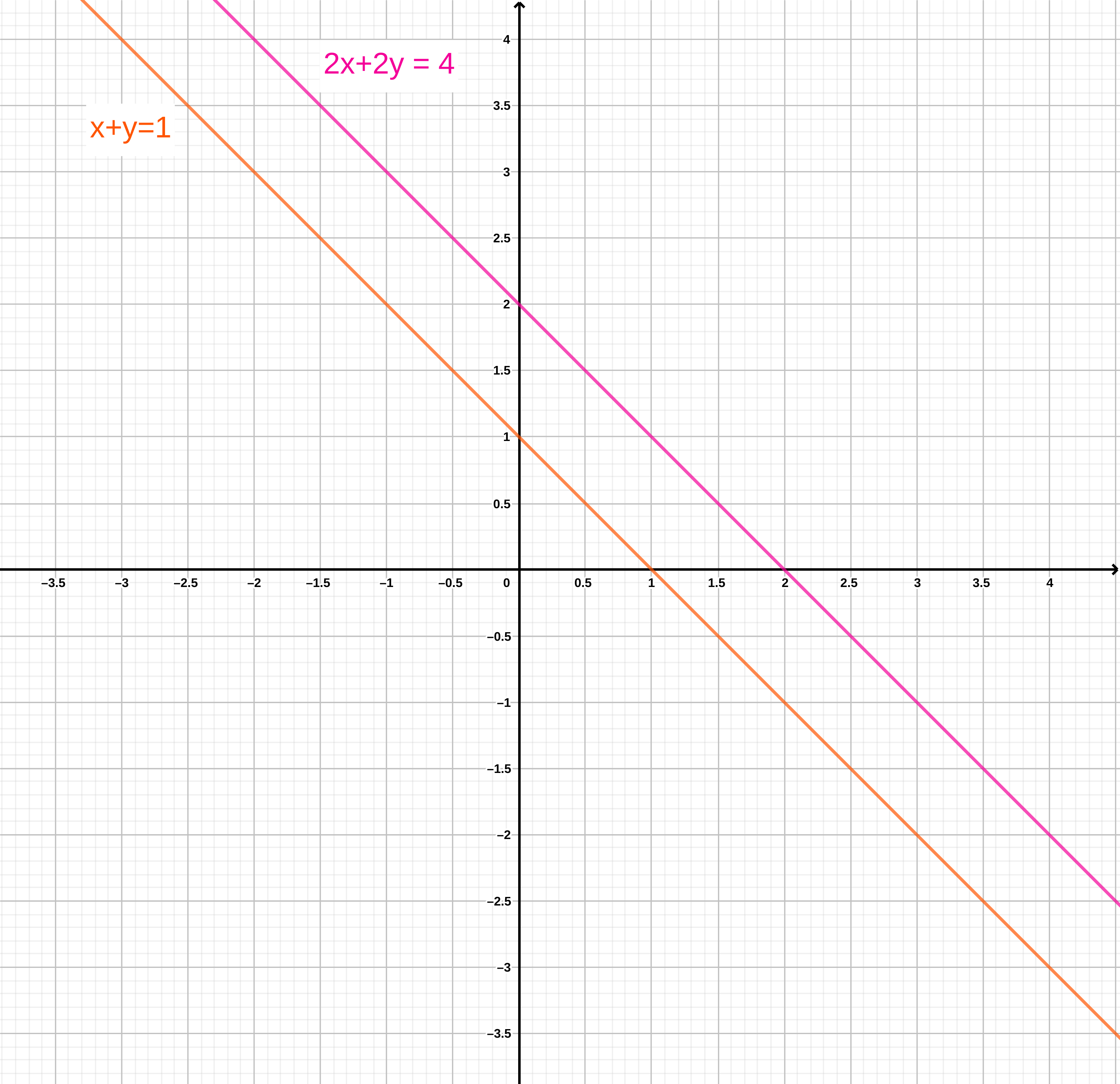
Figura 7.2: Representación gráfica de un sistema linea sin solución.
Si intentamos sumar o restar ambas ecuaciones terminamos con una contradicción. Tomemos por ejemplo la primera ecuación, multiplicada por \(-2\) para obtener:
\[(x + y = 1) \times -2 \rightarrow -2x-2y = -2\]
Y al sumarla a la segunda ecuación:
\[2x - 2x + 2y - 2y = 4-2 \rightarrow 0 = 2\]
7.1.4 Resolviendo sistemas lineales más complejos
Cualquier sistema de ecuaciones lineales son solución se puede revolver con los métodos que hemos aprendido hasta el momento. Como hemos visto, en estos métodos es fácil cometer errores, máxime con sistemas más complejos con muchas variables y ecuaciones. El método ideal sería aquel que:
- Evita manipulaciones riesgosas de las ecuaciones
- Permite encontrar todas las soluciones posibles
- Permite identificar sistemas sin solución
En la tarea de aprender a utilizar dichos métodos cabe resaltar que las incógnitas (\(x, y, z, \dots\)) juegan un papel secundario, lo más importante son los coeficientes de cada una en las distintas ecuaciones.
Para comenzar a visualizar un sistema lineal como matriz, echemos un vistazo al siguiente sistema:
\[\begin{align} x+y+z+t & = 1 \\ x-y-z+t & = 3 \\ -x-y+z-t & = 1\\ -3x+y-3z-3t &= 4 \end{align}\]
cuyos coeficientes podemos representar en una matriz como:
\[A = \left[ \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 &-1 &-1 & 1 \\ -1&-1 & 1 &-1 \\ -3& 1 &-3 &-3 \end{array} \right]\]
Nota que cada columna corresponde con cada una de las variables \(x, y, z, t\), y los números que contiene la matriz \(A\) son sus coeficientes. Usando este mismo arreglo, podemos representar todo el sistema de ecuaciones como el producto de un vector \(x, y, z, t\) y la matriz \(A\):
\[\begin{equation} \left[ \begin{array} {r} x \\ y \\ z \\ t \end{array} \right] \left[ \begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 &-1 &-1 & 1 \\ -1&-1 & 1 &-1 \\ -3& 1 &-3 &-3 \end{array} \right] = \left[\begin{array}{r} 1 \\ 3 \\ 1 \\ 4 \end{array}\right] \tag{7.1} \end{equation}\]
Dado que para las operaciones necesarias para resolverlo, sólo necesitamos la matriz de coeficientes \(A\) y el vector de equivalencias podemos representar el sistema con su matriz aumentada:
\[\begin{equation} \left[ \begin{array}{rrrr|l} 1 & 1 & 1 & 1 & 1\\ 1 &-1 &-1 & 1 & 3\\ -1&-1 & 1 &-1 & 1\\ -3& 1 &-3 &-3 & 4 \end{array} \right] \tag{7.2} \end{equation}\]
Para resolver sistemas como este necesitamos aprender a hacer algunas operaciones con filas que no alteran el estado del sistema lineal:
- Intercambiar filas
- Multiplicar una fila por un escalar \(c \neq 0\)
- Sumar dos filas
Ninguna de estas operaciones afectan las soluciones posibles del sistema (si las hay). Utilizando estas operaciones, la meta es transformar la matriz aumentada ((7.2)), en un a matriz que contenga ceros bajo la diagonal (Triángulo superior), y así poder sustituir los valores comenzando con la última fila. El sistema de ecuaciones (7.1), no tiene solución, por lo que solamente nos sirve, por el momento para establecer los conceptos. A continuación lo aplicamos con un sistema más sencillo.
7.1.5 Ejemplo
Dado el sitema linea:
\[\begin{align} 2x - 1y + 3z &= 9\\ 3x + 5y - z &= 10\\ 4x + 2y - 3z &= -1 \end{align}\]
la matriz aumentada es:
\[\begin{equation} \left[ \begin{array}{rrr|l} 2 & -1& 3 & 9 \\ 3 & 5 &-1 & 10\\ 4 & 2 &-3 &-1 \end{array} \right] \begin{array} \ (F_1) \\ (F_2) \\ (F_3) \end{array} \end{equation}\]
A continuación se muestra en el lado izquierdo, las operaciones correspondientes a las filas de las matrices:
\[\begin{equation} \begin{array}{r} (F_1) \\ -3(F_1)+2(F_2) \\ 2(F_1)-(F_3) \end{array} \left[ \begin{array}{rrr|r} 2 &-1 & 3 & 9 \\ 0 &13 &-11&-7 \\ 0 &-4 & 9 &19 \end{array} \right] \begin{array}{r} \ (F_4) \\ (F_5) \\ (F_6) \end{array} \end{equation}\]
Ahora la fila 1 se llama \((F_4)\), hicimos \(-3(F_1)+2(F_2)\) para eliminar el coeficiente \(a_{2,1} = 3\), y ahora lo llamamos \((F_5)\). Lo único que debemos hacer ahora, es encontrar cómo eliminar \(a_{2,3}\) en \((F_6)\), para obtener la matriz con ceros bajo la diagonal:
\[\begin{equation} \begin{array}{r} (F_4) \\ (F_5) \\ 4(F_5)+13(F_6) \end{array} \left[ \begin{array}{rrr|r} 2 &-1 & 3 & 9 \\ 0 &13 &-11&-7 \\ 0 & 0 &73 &219 \end{array} \right] \begin{array}{r} (F_7) \\ (F_8) \\ (F_9) \end{array} \end{equation}\]
A partir de aquí, tenemos una ecuación on una sola variable:
\[73z = 219\] Con la cual podemos sustituir desde \((R_9)\) hacia \((R_7)\) para obtener los valores de \(x\) y \(y\) que satisfacen al sistema lineal.
7.1.6 Sistemas indeterminados
Cuando hay más variables que ecuaciones, no es posible encontrar una solución única al sistema, veamos un ejemplo de estos sistemas:
\[\begin{align} 2x+2y-z &= 1 \\ 2x-y+z &= 2 \end{align}\]
cuya matriz aumentada es:
\[\begin{equation} \left[ \begin{array}{rrr|r} 2 & 2 & -1& 1 \\ 2 & -1& 1 & 2 \end{array} \right] \begin{array} (F_1) \\ (F_2) \end{array} \end{equation}\]
Lo primero que notamos es que, al haber más variables que ecuaciones, la matriz de coeficientes, tiene más columnas que filas. Entonces, vamos a comenzar por eliminar el coeficiente \(a_{2,1} = 2\), haciendo \((F_1)-F_2\):
\[\begin{equation} \begin{array}{r} (F_1) \\ (F_1) - (F_2) \end{array} \left[ \begin{array}{rrr|r} 2 & 2 &-1 & 1\\ 0 & 3 &-2 &-1 \end{array} \right] \begin{array}{r} (F_3) \\ (F_4) \end{array} \end{equation}\]
A partir de este punto sólo podemos expresar las soluciones para \(x\) y \(y\) en términos de \(z\):
\[\begin{align} 2x + 2y - z &= 1 \\ 3y - 2z & = -1 \end{align}\]
Por lo tanto:
\[y = - \frac{1}{3} + \frac{2}{3}z\]
y sustituyendo \(y\) en la primera ecuación encontramos que:
\[x = \frac{5}{6} - \frac{1}{6}z\]
Para reportar un conjunto de soluciones para todo el sistema, podemos crear una variable ficticia \(t = z\), con lo que la solución al sistema es:
\[\left\{(x, y, z): x = \frac{5}{6} - \frac{1}{6}z, y = - \frac{1}{3} + \frac{2}{3}z, z = t \right\}\]
7.2 Operaciones elementales con matrices
Las operaciones elementales con matrices son similares a las aritméticas tradicionales. Para ejemplificarlas aquí denotamos a una matriz cualquiera con letras mayúsculas.
7.2.1 Suma de matrices
Si las matrices \(A\) y \(B\) tienenlas mismas dimensiones \(m \times n\) (\(m\) = número de filas, \(n\) = número de columnas):
\[A + B = C\] La adición de \(A\) con \(B\) resulta en una tercera matriz \(C\) con dimensiones \(m \times n\), tanto si \(m = n\) como \(m \neq n\), es decir si las matrices \(A\) y \(B\) son cuadradas (\(m = n\)) como rectangulares.
Para esto tenemos que considerar qué sucede con los elementos de \(A\) y \(B\) dentro de \(C\):
\[\begin{equation} A = \left[ \begin{array}{ccc} a_{1, 2} & \dots & a_{1, n} \\ \vdots & \ddots & \vdots \\ a_{n, 1} & \dots & a_{n, n} \end{array} \right] \end{equation}\]
\[\begin{equation} B = \left[ \begin{array}{ccc} b_{1, 2} & \dots & b_{1, n} \\ \vdots & \ddots& \vdots \\ b_{n, 1} & \dots & b_{n, n} \end{array} \right] \end{equation}\]
\[\begin{equation} C = \left[ \begin{array}{ccc} a_{1, 2} + b_{1, 2} & \dots & a_{1, n} + b_{1, n} \\ \vdots & \ddots & \vdots \\ a_{n, 1} + b_{n, 1} & \dots & a_{n, n} + b_{n, n} \end{array} \right] \end{equation}\]
Es claro que también:
\[B+A = C\]
Lo cual resulta importante resaltar pues la conmutatividad no funciona para la multiplicación de matrices. Otras cualidades de la adición de matrices, dadas las condiciones de dimensiones son:
- \((A+B)+C=A+(B+C)\)
- \(A + 0 = A\)
7.2.2 Multiplicación por un escalar
Es frecuente multiplicar una matriz por una constante \(c\), tal que \(c \times A = cA\):
\[\begin{equation} c \times A = \left[ \begin{array}{ccc} c \cdot a_{1, 2} & \dots & c \cdot a_{1, n} \\ \vdots & \ddots & \vdots \\ c \cdot a_{n, 1} & \dots & c \cdot a_{n, n} \end{array} \right] \end{equation}\]
7.2.3 Transposición
La transposición es el cambio de filas y columnas por columnas y filas, por ejemplo:
\[\begin{equation} A = \left[ \begin{array}{rrr} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array} \right] \end{equation}\]
Con lo que la matriz \(A\) transpuesta \(A^T = A'\) es:
\[\begin{equation} A' = \left[ \begin{array}{rr} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{array} \right] \end{equation}\]
7.2.4 Multiplicación de matrices
Para entender la multiplicación de matrices es necesario definirla, pues es más complicada que cualquiera de las operaciones que hemos visto anteriormente.
Supongamos que \(C\) es una matriz producto de la multiplicación de las matrices \(A\) y \(B\):
\[C = AB\]
Para que esto sea posible es necesario que \(A\) y \(B\) tengan dimensiones específicas pues:
\[\begin{equation} C = \left[ \begin{array}{rrr} & & \\ & c_{ij} & \\ & & \end{array} \right] = \left[ \begin{array}{ccc} & & & \\ a_{i, 1} & \dots & a_{i, l} \\ & & & \end{array} \right] \times \left[ \begin{array}{ccc} & b_{1, j} & \\ & \vdots & \\ & b_{l, j} & \end{array} \right] \tag{7.3} \end{equation}\]
Como resulta evidente, el número de columnas de la matriz \(A\) debe ser igual al número de filas de la matriz \(B\). De modo que podemos resumir que las dimensiones deben ser:
- \(A \rightarrow m \times l\)
- \(B \rightarrow l \times n\)
7.2.4.1 Ejemplos
\[\begin{equation} A = \left[ \begin{array} \ 1 & 2 & 3 \\ -1& 0 & 4 \end{array} \right] \end{equation}\]
y
\[\begin{equation} B = \left[ \begin{array} \ 1 & 2 & 3 & -3\\ 0 &-1 & 4 & 0 \\ -1& 0 &-2 & 1 \end{array} \right] \end{equation}\]
Solución:
\[\begin{equation} C = AB = \left[ \begin{array} \ 1 & 2 & 3 \\ -1& 0 & 4 \end{array} \right] \left[ \begin{array} \ 1 & 2 & 3 & -3\\ 0 &-1 & 4 & 0 \\ -1& 0 &-2 & 1 \end{array} \right] \end{equation}\]
Como vimos en la definición de multiplicación, tenemos que muiltiplicar las filas de \(A\) por las columnas de \(B\), para así obtener los elementos de \(C\). Hagamos entonces las operaciones elemento por elemento:
\[\begin{equation} c_{1, 1} = \left[ \begin{array}{rrr} \ 1 & 2 & 3 \end{array} \right] \left[\begin{array} \ 1 \\ 0 \\ -1 \end{array} \right] = (1)(1) + (2)(0) + (3)(-1)= -2 \end{equation}\]
\[\begin{equation} c_{1, 2} = \left[ \begin{array} 1 & 2 & 3 \end{array} \right] \left[ \begin{array} \ 2 \\ -1 \\0 \end{array} \right] = (1)(2) + (2)(-1) + (3)(0) = 0 \end{equation}\]
Y así sucesivamente para obtener:
\[\begin{equation} C = \left[ \begin{array} \ c_{1, 1} & c_{1, 2} & c_{1, 3} & c_{1, 4} \\ c_{2, 1} & c_{2, 2} & c_{2, 3} & c_{2, 4} \end{array} \right] = \left[ \begin{array} \ -2 & 0 & 5 & 0 \\ -5 & -2 & -11 & 7 \end{array} \right] \end{equation}\]
El resultado es una matriz con tantas filas como \(A\) y tantas columnas como \(B\). Es decir que si las dimensiones de \(A\) son \(m \times l\), y las de \(B\) son \(l \times n\), \(C\) tendrá dimensiones \(m \times n\).
7.3 Determinantes y matrices inversas
7.3.1 Matriz identidad
Antes de continuar, consideremos la posible existencia de una matriz \(I\) tal que \(A I = A\), es decir, una matriz que multiplicada por otra matriz de como resultado la matriz original. Esta matriz se conoce como la matriz identidad, y consiste de una matriz cuadrada con ceros en todas las posiciones excepto en la diagonal, por ejemplo:
\[\begin{equation} I = \left[ \begin{array}{ccc} \ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right] \end{equation}\]
Por el contrario, una matriz inversa es quella matriz \(A^{-1}\), tal que \(AA^{-1} = I\), al multiplicarla por una matriz cualquiera \(A\) da como resultado la matriz identitaria.
7.3.2 Matriz inversa
La utilidad de este concepto se puede ejemplificar con un sistema de una sola ecuación:
\[2x = 10\]
Esta ecuación podemos concebirla como el producto de dos vectores con dimensiones \(1 \times 1\). Para resolverla es necesario multplicar ambos lados de la ecuación por el inverso del coeficiente de \(x\), de modo que:
\[2^{-1} \cdot 2x = 2^{-1} \cdot 10\]
\[x = \frac{1}{5}\]
Por lo tanto, si tenemos que para un sistema lineal la matriz cuadrada \(A\) de coeficientes puede ser invertida como \(A^{-1}\), esta última contiene la solución al sistema mismo:
\[XA = B\]
\[A^{-1}XA = A^{-1}B \rightarrow X = A^{-1}B\]
7.3.2.1 Definción de matriz inversa
Una matriz inversa de \(A\) es aquella matriz \(B\) que:
\[AB = BA = I_n\]
al ser multiplicada por \(A\) tiene como resultado la matriz identidad \(I_n\), con dimensiones \(n \times n\). La matriz inversa de \(A\) también recibe, como ya se mencionó el nombre \(A^{-1}\). Cuando se puede obtener la matriz \(A^{-1}\) de \(A\), se dice que esta última es invertible o no-singular, de lo contrario se le llama singular. Cabe resaltar que la matriz inversa \(A^{-1}\) es única para \(A\). Si llegaran a existir dos matrices inversas \(B\) y \(C\) de \(A\), entonces \(B=C\).
7.3.2.2 Obteniendo una matriz inversa
Para obtener una matriz inversa, también tenemos que resolver un sistema de ecuaciones lineales. Supongamos que \(A\) es una matriz de \(2 \times 2\):
\[\begin{equation} A = \left[\begin{array}{ccc} a_{1, 1} & a_{1, 2} \\ a_{2, 1} & a_{2, 2} \end{array} \right] \end{equation}\]
Recordemos que \(A\) es la matriz de coeficientes para las variables \(x_1, x_2, \dots, x_n\). Entonces la matriz inversa de \(A\) es:
\[\begin{equation} B = \left[\begin{array}{ccc} b_{1, 1} & b_{1, 2} \\ b_{2, 1} & b_{2, 2} \end{array} \right] \end{equation}\]
Por lo tanto la ecuación a resolver es:
\[\begin{equation} \left[\begin{array}{ccc} a_{1, 1} & a_{1, 2} \\ a_{2, 1} & a_{2, 2} \end{array} \right] \left[\begin{array}{ccc} b_{1, 1} & b_{1, 2} \\ b_{2, 1} & b_{2, 2} \end{array} \right] = \left[\begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right] \end{equation}\]
donde las incógnitas son los elementos \(b_{1,1}, \dots b_{n,n}\) de \(B\), la matriz inversa.
7.3.2.2.1 Ejemplo
Tenemos que encontrar la matriz inversa de la matriz de coeficientes:
\[\begin{equation} A = \left[\begin{array}{ccc} 2 & 5 \\ 1 & 3 \end{array} \right] \end{equation}\]
Por lo tanto el sistema de ecuaciones a resolver es:
\[\begin{equation} \left[\begin{array}{ccc} 2 & 5 \\ 1 & 3 \end{array} \right] \left[\begin{array}{ccc} b_{1, 1} & b_{1, 2} \\ b_{2, 1} & b_{2, 2} \end{array} \right] = \left[\begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right] \end{equation}\]
Para ver las ecuaciones a resolver para \(B\), tenemos que multiplicar \(AB\), con lo que obtenemos:
\[\begin{align} 2 b_{1,1} + 5b_{2,1} = 1\ (F_1) & & 2b_{1, 2} + 5b_{2,2} = 0\ (F_1) \\ \notag b_{1, 1} + 3b_{2,1} = 0\ (F_2) & & b_{1, 2} + 3b_{2, 2} = 1 (F_2 ) \notag \end{align}\]
Utilizando los métodos que ya conocemos, podemos obtener las soluciones:
\[\begin{equation} B = \left[ \begin{array} \ b_{1, 1} & b_{1, 2} \\ b_{2, 1} & b_{2, 2} \end{array} \right] = \left[ \begin{array} \ 3 & -5 \\ -1 & 2 \end{array} \right] \end{equation}\]
7.3.3 Determinante de una matriz
Para continuar con este tema revisaremos rápidamente, qué es y qué hacen los vectores. Por ejemplo, la matriz:
\[ A = \left[ \begin{array}{cc} 3 & 0 \\ 0 & 2 \end{array} \right] \]
puede concebirse como dos vectores \(A_1 = \left[\begin{array}{c}3 \\ 0 \end{array} \right]\) y \(A_2 = \left[\begin{array}{c}0 \\ 2 \end{array} \right]\). Cada uno de estos vectores pueden representarse geométricamente como indicaciones de movimiento en el plano cartesiano. El vector \(A_1\) indica \(3\) pasos en dirección \(x\) y \(0\) en dirección \(y\). \(A_2\) indica \(0\) pasos en dirección \(x\) y \(2\) en dirección \(y\).
Cuando representamos estos vectores en el plano vemos que \(A_1\) está alineado con el eje \(x\) y \(A_2\) con el \(y\), y el área formada por ambos corresponde al producto de la primera diagonal de \(A\), \(3 \times 2\) (figura 7.3).
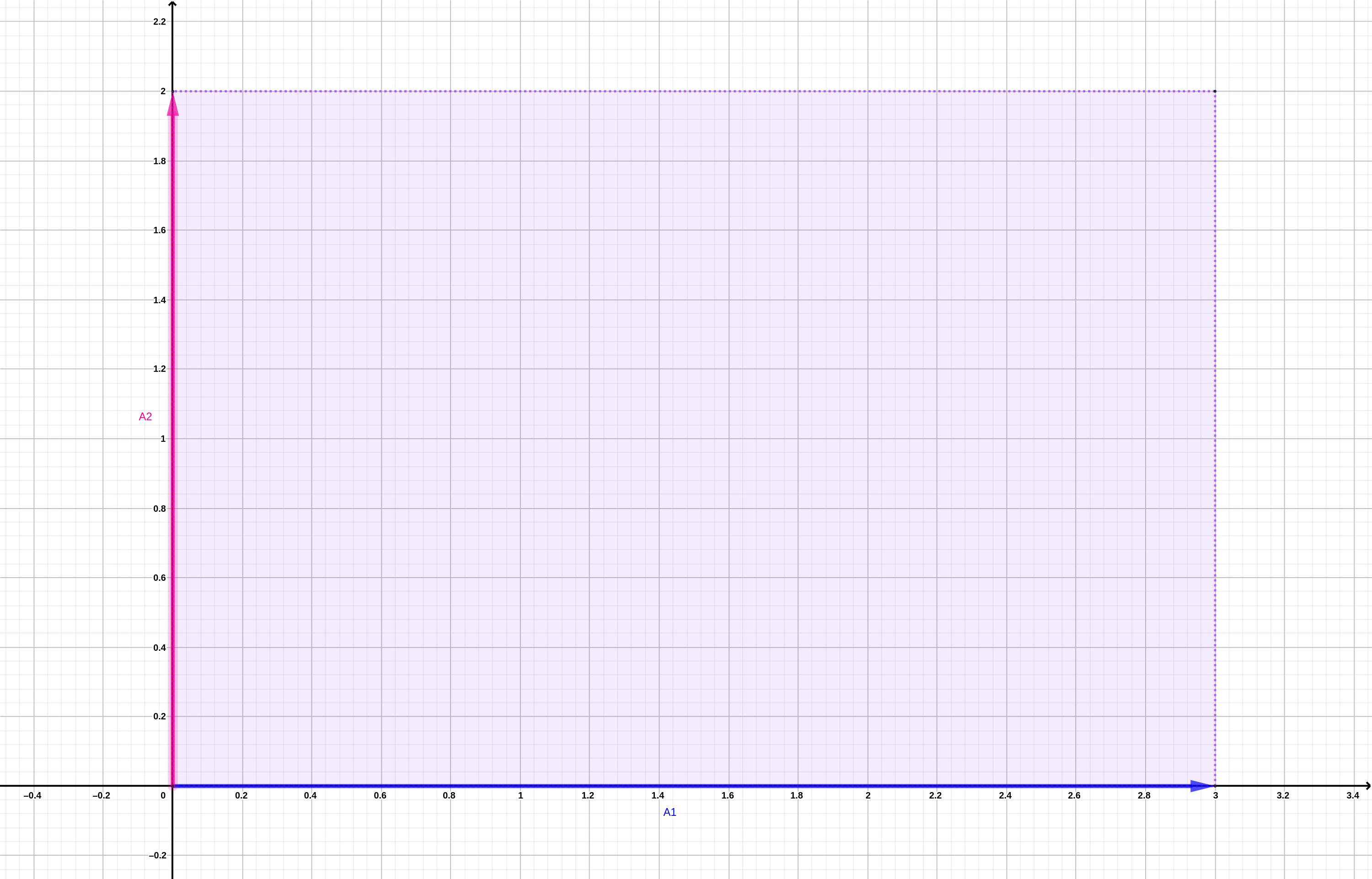
Figura 7.3: Representación gráfica del determinante de la matriz A
Cuando las matrices utilizadas en una transformación lineal (que multiplican a un vector, por ejemplo), no tienen ceros en las casillas fuera de las diagonales, el área proyectada por los vectores será un rombo, por lo que hay que sustraer el área fuera del producto de la diagonal. Por ejemplo la matriz
\[ A = \left[ \begin{array}{cc} 1 & 1 \\ \frac{1}{2} & 2 \end{array} \right] \]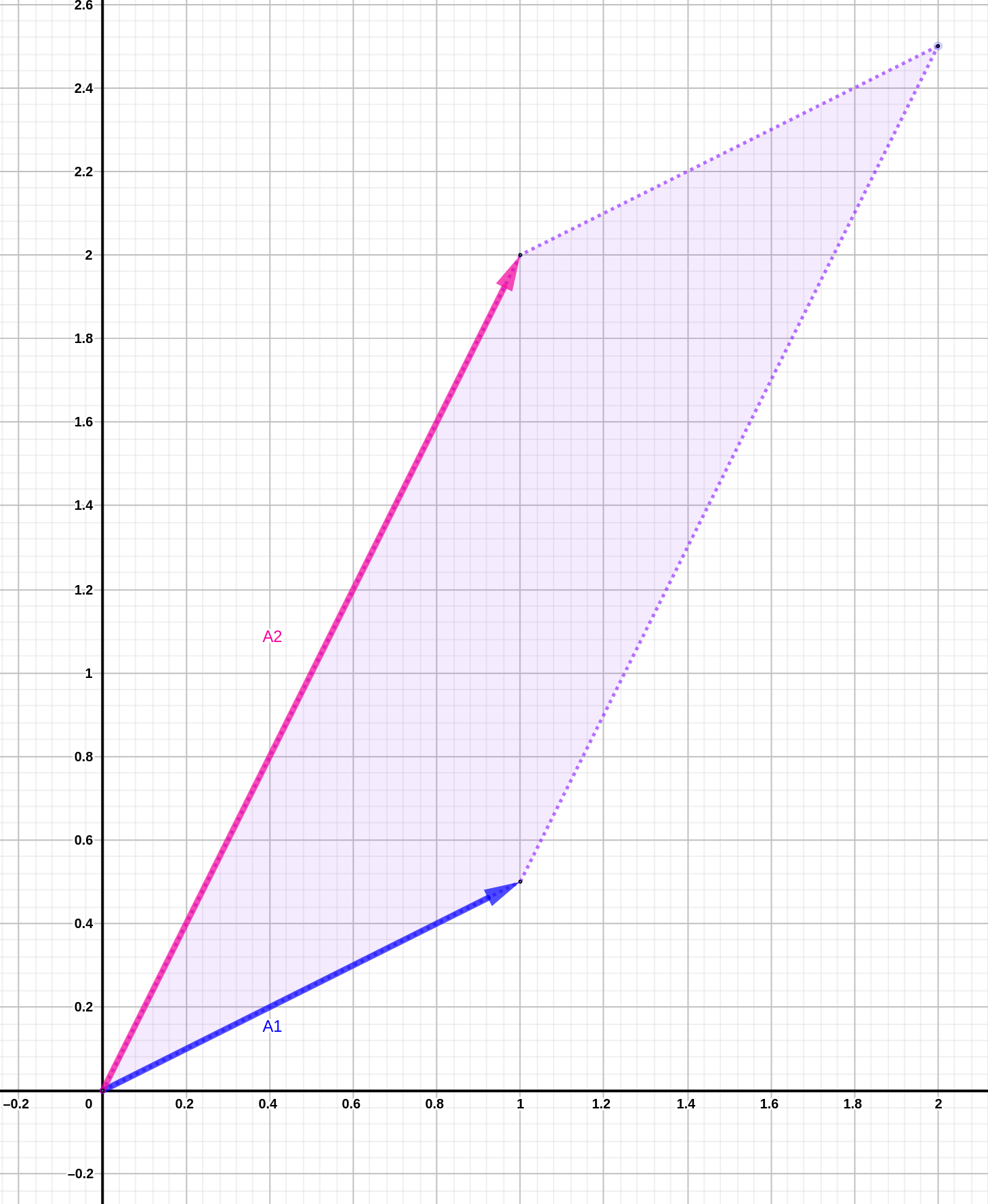
Figura 7.4: Representación del área formada por matriz sin ceros fuera de la diagonal
con lo que el área formada por los vectores es \(1 \times 2 - 1/2 \times 1= 3/2\). El área formada por una matriz recibe el nombre de determinante (\(\mathrm{det}A\) ó \(|A|\)), puesto que es el efecto neto de la transformación lineal producida por la matriz en el vector a que afecta.
El determinante puede utilizarse con muchos propósitos, uno de ellos es invertir una matriz. Para cualquier matriz \(A\) con dimensiones \(2 \times 2\), \(A\) es invertible si el área que ésta produce es mayor a \(0\).
De manera más general:
\[\begin{equation} A = \left[ \begin{array} \ a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \end{array} \right] \tag{7.4} \end{equation}\]
\(A^{-1}\) existe si \(a_{1,1}a_{2,2} - a_{1,2}a_{2,1} \neq 0\) (figura 7.5)

Figura 7.5: Representación de matriz con determinante de 0.
Para calcular una matriz inversa usando el determinante, necesitamos encontrar la matriz adjunta transpuesta. Para una matriz de \(2 \times 2\) como (7.4):
\[\begin{equation} A^{-1} = \frac{1}{a_{1,1}a_{2,2} - a_{1,2}a_{2,1}} \left[ \begin{array} \ a_{2,2} & -a_{1,2} \\ -a_{2,1} & a_{1,1} \end{array} \right] \tag{7.5} \end{equation}\]
La expresión \(a_{1,1}a_{2,2} - a_{1,2}a_{2,1}\) para una matriz \(A\) de \(2 \times 2\) se conoce como el determinante y se denota como \(\mathrm{det} A\) ó \(|A|\).
Es posible calcular determinantes para cualquier matriz \(A\) con dimensiones \(n \times n\), y en todos los casos, es posible obtener \(A^{-1}\) si \(\mathrm{det}A \neq 0\). Las fórmulas para calcular el determinante de cualquier matriz se van complicando considerablemente conforme aumenta su tamaño, por lo que es necesario utilizar una calculadora de determinantes.
Aquí nos limitaremos a las fórmulas para determinantes de \(2\times 2\) (ecuación (7.5). La figura 7.6 muestra el procedimiento para una matrix de \(3 \times 3\).
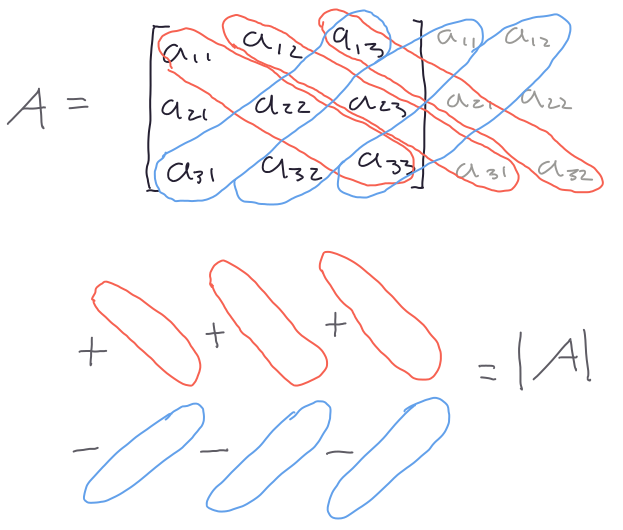
Figura 7.6: Esquema del procedimiento para calcular el determinante de una matriz de 3 x 3.
7.4 Valores propios
Para hablar de vectores y valores propios necesitamos definir a un vector como una matriz con una sola columna y \(n\) filas. Todos los ejemplos que veremos aquí son de vectores de \(2 \times 1\).
Los vectores en el sentido en que los trataremos aquí, representan indicaciones de movimiento en el plano cartesiano. Por ejemplo el vector:
\[\left[ \begin{array}{cc} 2 \\ 3 \end{array} \right]\]
indica un movimiento de dos posiciones a la derecha en el eje \(x\) y tres posiciones arriba en el eje \(y\) (vector \(\mathbf{u}\) en la figura )
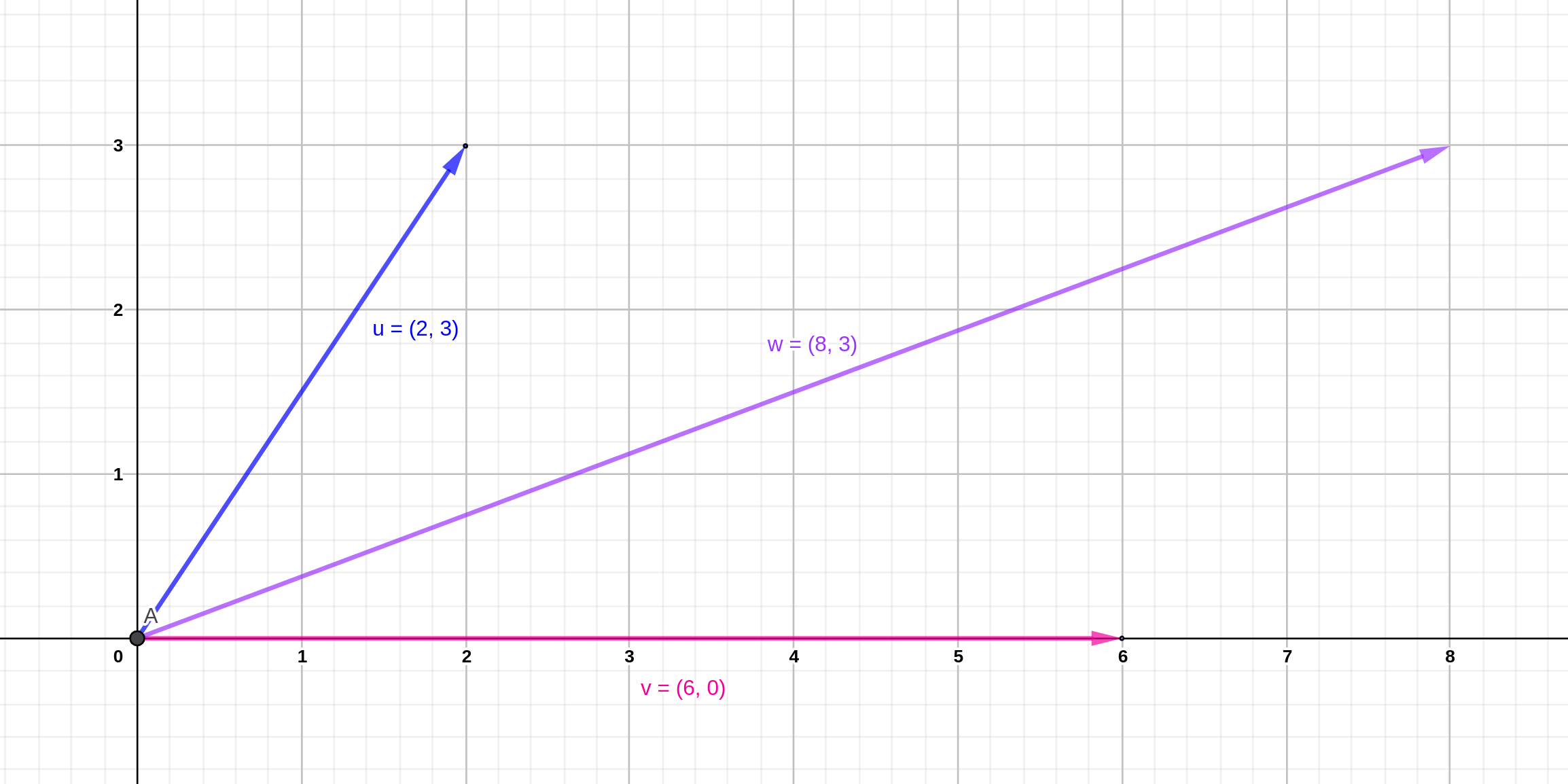
Figura 7.7: Ejemplos de vectores u = (2, 3), u=(6, 0) y w = u + v.
Las operaciones con vectrores son iguales que las operaciones con matrices, de modo que el vector \(\mathbf{w}\) de la figura 7.7 es:
\[\mathbf{w} =\left[ \begin{array}{c} 2 \\ 3 \end{array} \right] + \left[ \begin{array}{c} 6 \\ 0 \end{array} \right] = \left[ \begin{array}{c} 2 + 6 \\ 3 +0 \end{array} \right] = \left[ \begin{array}{c} 8 \\ 3 \end{array} \right]\]
Cuando multiplicamos un vector cualquiera por un escalar, éste alargará el vector en relación a su magnitud, tal que :
\[ \mathbf{a} = 2 \times \mathbf{u} = \left[ \begin{array}{c} 4 \\ 6 \end{array} \right] \]
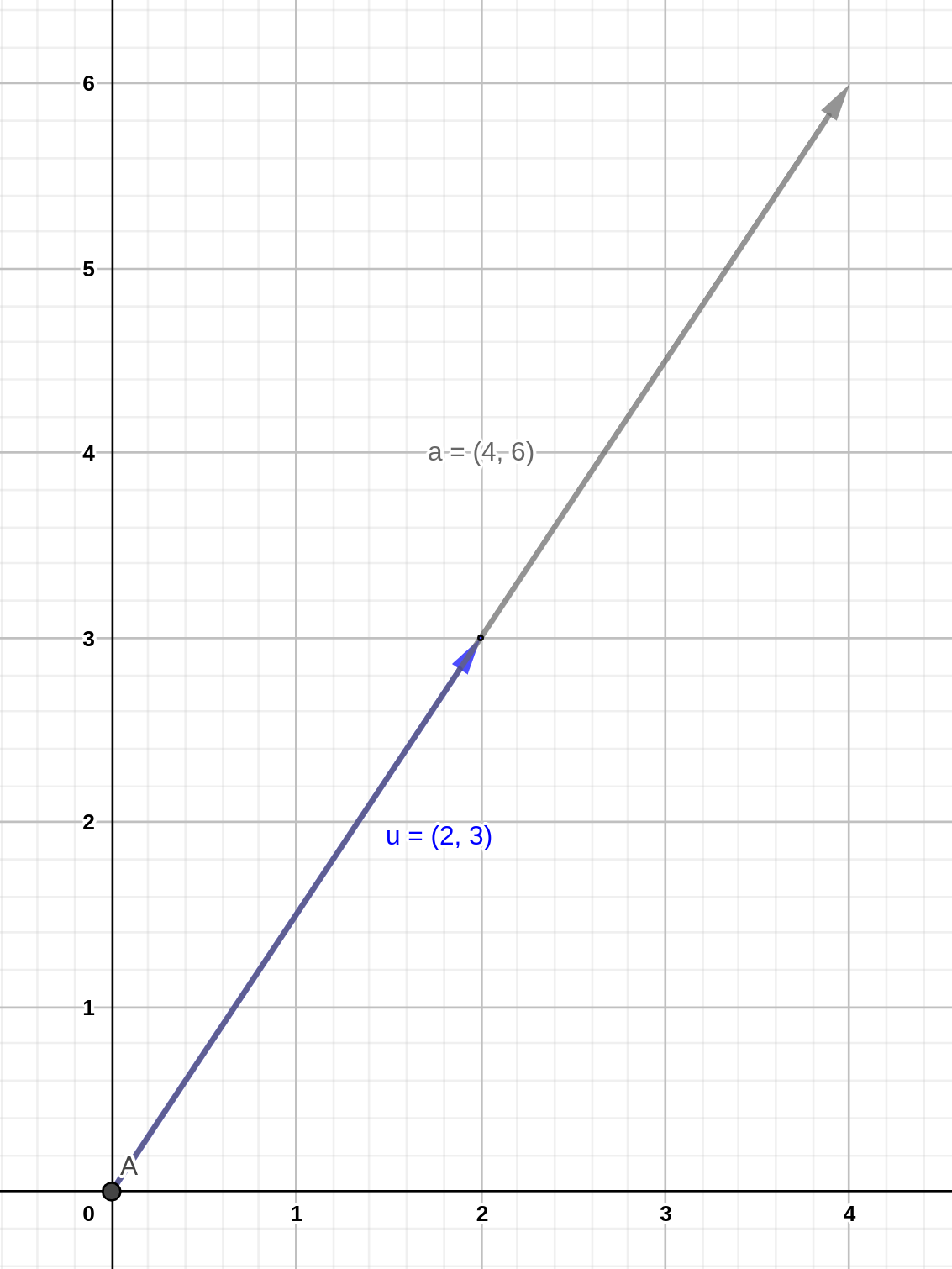
Figura 7.8: Multiplicación de vector por un escalar.
La operación que nos más concierne, sin embargo, en el caso de los valores y vectores propios es la multiplcación de un vector \(\mathbf{x}\) por una matriz \(A\).
Con base en las reglas de multiplicación sabemos que para el vector \(\mathbf{x}\) con dimensiones \(2 \times 1\) y la matriz \(A\) con dimensiones \(2 \times 2\), el producto \(A \mathbf{x}\) tendrá dimensiones de \(2 \times 1\). Dicha multiplicación se conoce como el mapa de \(\mathbf{x}\) y se escribe:
\[\begin{equation} \mathbf{x} \mapsto A\mathbf{x} \tag{7.6} \end{equation}\]
Por ejemplo:
\[\begin{equation} \left[ \begin{array}{cc} 3 & 2 \\ 1 & 4 \end{array} \right] \cdot \left[ \begin{array}{c} 1 \\ 2 \end{array} \right]= \left[ \begin{array}{c} 7 \\ 9 \end{array} \right] \end{equation}\]
donde \(\mathbf{x}\) es el vector \((1, 2)\), y el mapa \(A \mathbf{x}\) es el vector \((7, 9)\).
El concepto de vector y valor propio está basado en \(\mathbf{x} \mapsto A \mathbf{x}\). Específicamente \(A \mathbf{x}\) es el vector propio y el valor propio es una constante que satisface:
\[\begin{equation} A \mathbf{x} = \lambda \mathbf{x} \tag{7.7} \end{equation}\]
Este tipo de operaciones tiene muchas aplicaciones, entre ellas está el resolver sistemas de ecuaciones. Aunque sólo veremos ejemplos con vectores de \(2 \times 1\), todos los ejemplos son generalizables a vectores con cualquier número de filas.
Para calcular \(\lambda\) al igual que hicimos para \(A^{-1}\), comenzamos por resolver la ecuación (7.7):
\[A \mathbf{x} = \lambda I \mathbf{x} \rightarrow (A - \lambda I) \mathbf{x} = 0\] La parte \(\lambda I \mathbf{x}\) se debe a que \(I \mathbf{x} = \mathbf{x}\), pero necesitamos una matriz cuadrada para resolver a continuación.
Dado que \(\mathbf{x} \neq 0\), necesitamos que \(A - \lambda I\) sea singular (\(|A| = 0\)), de modo que necesitamos encontrar un valor de \(\lambda\) que satisfaga \(\det (A - \lambda I) = 0\). Entonces si nuestra matriz:
\[A = \left[ \begin{array}{cc} 1 & 2 \\ 3 & 2 \end{array} \right]\]
entonces:
\[A - \lambda I = \left[ \begin{array}{cc} 1 - \lambda & 2 \\ 3 & 2 - \lambda \end{array} \right]\]
cuyo determinante será:
\[\begin{align} (1 - \lambda)(2-\lambda) - (2)(3) &= 2 - 3 \lambda +\lambda^2 -6\\ & = \lambda^2 - 3 \lambda -4 \\ & = (\lambda + 1)(\lambda - 4) \end{align}\]
por lo tanto tenemos las soluciones \(\lambda_1 = -1\) y \(\lambda_2 = 4\). Como es evidente, los vectores propios \(A \mathbf{x}\) que satisfacen los valores propios no son únicos, pero cada valor propio \(\lambda\) está asociado a un vector propio. Para los sistemas lineales con más de dos variables habrá tantos valores propios como dimensiones.
7.5 Vectores propios
Como vimos anteriormente, los valores propios son independientes de los vectores, es decir, los valores reflejan una propiedad de las matrices. Para encontrar los vectores que satisfacen la propiedad:
\[A \vec{x} = \lambda \vec{x}\]
tenemos que resolver la ecuación para los valores de \(\lambda\). Pongamos por ejemplo la matriz
\[A = \left[\begin{array}{cc} 1 & 2 \\ 3 & 2 \end{array}\right]\]
tiene los valores propios \(\lambda_1 = -1\) y \(\lambda_2 = 4\), y la ecuación a resolver para obtener los vectores propios que corresponden con \(\lambda_1\) son:
\[\begin{equation} \left[\begin{array}{cc} 1 & 2 \\ 3 & 2 \end{array}\right] \left[\begin{array}{c} x_1 \\ x_2 \end{array} \right] = -1 \left[\begin{array}{c} x_1 \\ x_2 \end{array} \right] \end{equation}\]
pasando el lado izquierdo al derecho, factorizando el vector \(\vec{v}\), y multiplicando \(\lambda\) por la matriz identidad tenemos:
\[\begin{equation} \left( \left[\begin{array}{cc} 1 & 2 \\ 3 & 2 \end{array}\right] + \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right] \right) \left[\begin{array}{c} x_1 \\ x_2 \end{array} \right] = \vec{0} \end{equation}\]
y sumando las matrices tenemos:
\[\begin{equation} \left[\begin{array}{cc} 1 + 1 & 2 \\ 3 & 2 + 1 \end{array}\right] \left[\begin{array}{c} x_1 \\ x_2 \end{array} \right] = \vec{0} \end{equation}\]
Una vez encontrado el sistema, podemos resolverlo con el método de la matriz aumentada:
\[\begin{equation} \left[ \begin{array}{cc|c} 2 & 2 & 0 \\ 3 & 3 & 0 \end{array}\right] \begin{array}{c} (F_1) \\ (F_2) \end{array} \end{equation}\]
aunque si lo resolvemos con el método tradicional siempre llegaremos a la solución \(x_1 = 0; x_2 = 0\). Entonces necesitamos reducir la matrix por fila al modo Echelon. Este método consiste en realizar las operaciones con filas para reducir las filas inferiores a ceros. Por ejemplo, reemplazando \(F_2\) con \(3 F_1 - 2F_2\), y dividiendo \(F_1/2\):
\[\begin{equation} \left[ \begin{array}{cc|c} 1 & 1 & 0 \\ 0 & 0 & 0 \end{array}\right] \begin{array}{c} (F_3) \\ (F_4) \end{array} \end{equation}\]
Por lo tanto el vector propio para \(\lambda_1 = -1\) es \((1, 1)\). El proceso para encontrar el vector propio para \(\lambda_2\) es el mismo.