4 Unidad II: Introducción a los modelos determinísticos

4.1 La línea recta

Una línea recta se puede representar matemáticamente de varias maneras, la más común de ellas es por medio de una función. Una función, en cambio es una expresión matemática que indica una serie de operaciones (aritméticas por ejemplo), que serán aplicadas a un conjunto de números en sucesión (los números reales, p. ej.) para producir otro conjunto. Así la, función lineal más sencilla puede ser:

\[\begin{equation} y(x) = x \end{equation}\]

Lo que quiere decir que $y$ es una función de $x$, y cada valor de $y$ será igual a cada valor de $x$. En lenguaje matemático, el conjunto de números de $x$ se llama el dominio, y $y(x)$ el codominio. Algunas funciones lineales más complejas son:

\[\begin{equation} y(x) = ax \end{equation}\]

donde $a$ es una constante, lo que quiere decir que cada valor de $y(x)$ será producido por el producto $a \times x$. Finalmente, la expresión más común de una ecuación lineal es:

\[\begin{equation} y(x) = b + ax \end{equation}\]

donde $b$ también es una constante que se llama intercepto, y $a$ es la pendiente, pues esta última determina la inclinación de la línea recta representada en el plano cartesiano.

4.1.0.1 Representaciones gráficas de la recta

Comencemos por dar un repaso del plano cartesiano. Este consiste de la representación de dos conjuntos de números reales en los que representamos una función, como una regla de correspondencia entre los valores de cada conjunto, de modo que a cada valor de $x$ corresponde uno y sólo uno de los valores de $y$. Cada conjunto se puede representar como una recta, y cuando éstas se disponen perperdiculares dan origen al plano.

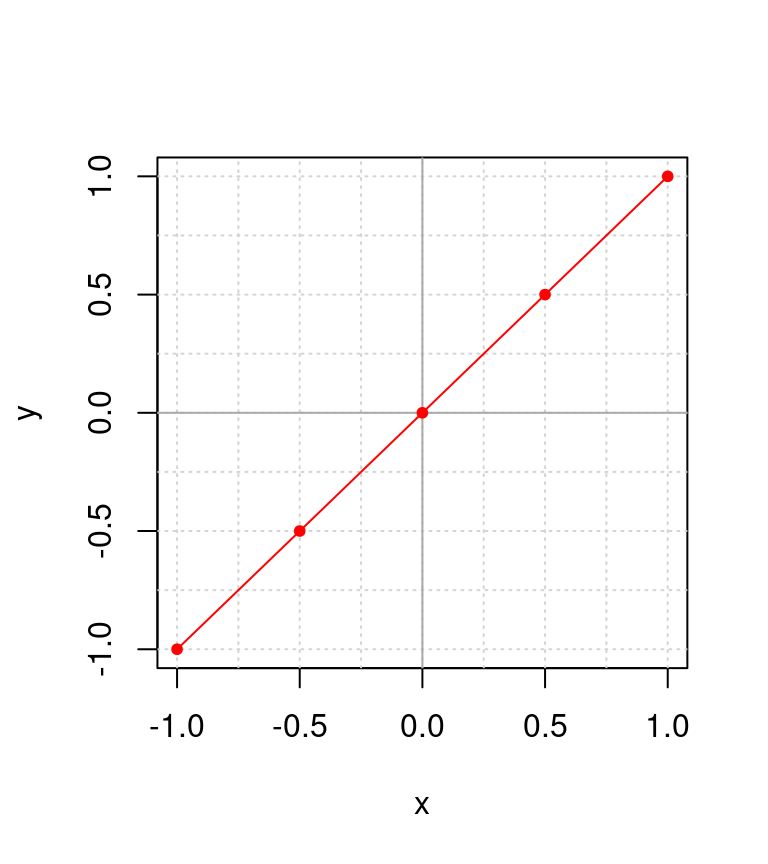
Ejemplo del plano cartesiado mostrando en rojo la correspondencia de valores para $y(x) = x$, donde los puntos corresponden a los pares de valores $(x = -1, y = -1), (-0.5, -0.5), (0, 0), (0.5, 0.5), (1, 1)$.

Figura 4.1: Ejemplo del plano cartesiado mostrando en rojo la correspondencia de valores para $y(x) = x$, donde los puntos corresponden a los pares de valores $(x = -1, y = -1), (-0.5, -0.5), (0, 0), (0.5, 0.5), (1, 1)$.

Ahora veamos, con un ejemplo gráfico por qué la constante $a$ recibe el nombre de pendiente.

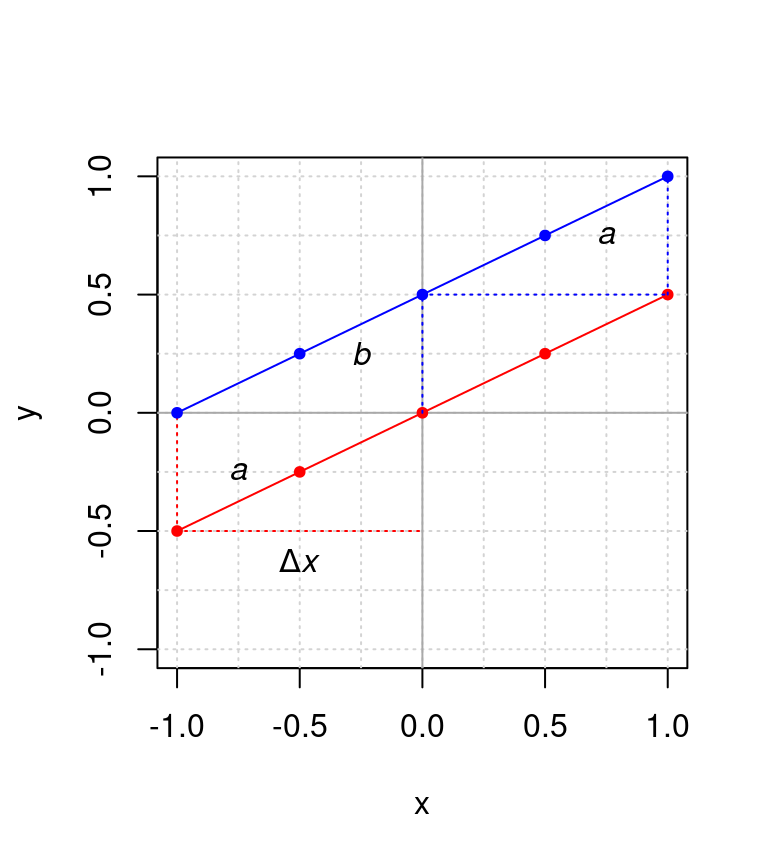
Gráficas de las funciones $y(x) = 0.5 x$ (en rojo) y $y(x) = 0.5 + 0.5 x$ (azul). Las líneas punteadas en colores indican el efecto de las constantes $a$ y $b$, mientas que Δ$x$ denota el cambio de una unidad de $x$.

Figura 4.2: Gráficas de las funciones $y(x) = 0.5 x$ (en rojo) y $y(x) = 0.5 + 0.5 x$ (azul). Las líneas punteadas en colores indican el efecto de las constantes $a$ y $b$, mientas que Δ$x$ denota el cambio de una unidad de $x$.

Como podemos ver, de manera más general, la línea recta es generada por una regla de correspondencia muy sencilla, un conjunto de valores $X$ son multiplicados por un escalar $a$, a los que se les puede añadir un intercepto $b$. El intercepto siempre es el valor de $y(x)$ cuando $x = 0$.

Ya se podrán imaginar que puede existir un sinnúmero de modelos lineales distintos, por ejemplo si $y$ es una función de un gran número de conjuntos $X$:

\[\begin{equation} y(x_1, x_2, \dots, x_{n-1}, x_n) = b + a_1 x_1 + a_2 x_2 + \dots + a_{n-1} x_{n-1} + a_n x_n \end{equation}\]

Gráficamente, estamos prácticamente limitados a explorar $y(x_1, x_2)$, pero existen muchas herramientas matemáticas para entender modelos lineales más complejos que veremos más adelante. Estas herramientas y las implicaciones generales de la simplicidad del modelo lineal lo hacen uno de los modelos más útiles con que contamos para estudiar matemáticamente fenómenos dinámicos (que cambian de estado a lo largo del tiempo), como para estudiarlos de manera probabilística (con estadística). De hecho, el modelo lineal nos puede servir para entender modelos, como la parábola y el exponencial, que geométricamente no se parecen a la línea recta.

4.2 La parábola

Geométricamente, la parábola es muy distinta de la recta:

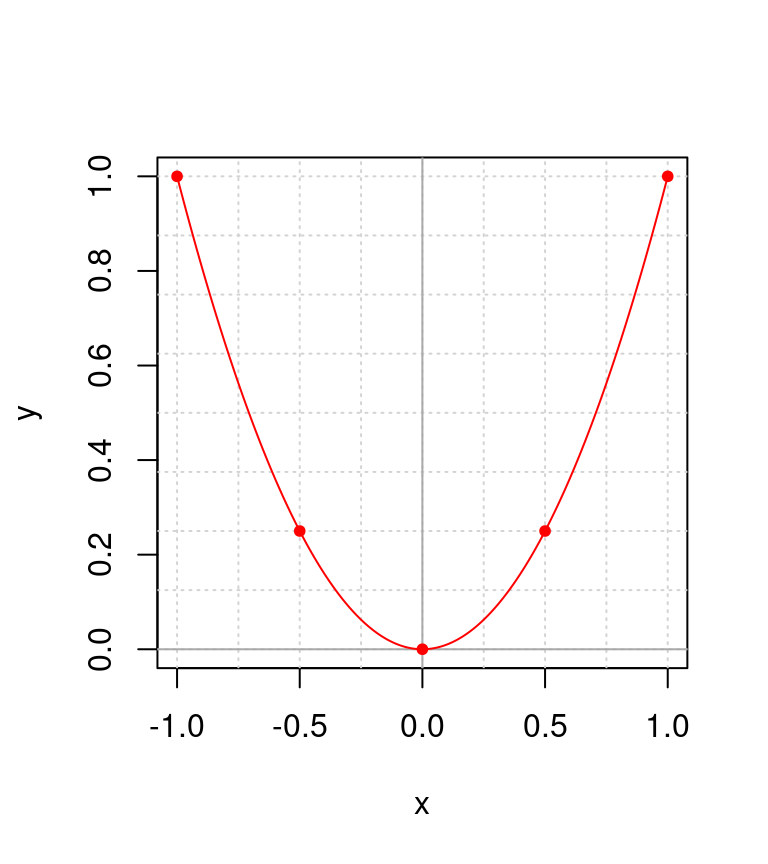
Ejemplo del plano cartesiado mostrando en rojo la correspondencia de valores para $y(x) = x^2$, donde los puntos corresponden a los pares de valores $(x = -1, y = 1), (-0.5, 0.25), (0, 0), (0.5, 0.25), (1, 1)$.

Figura 4.3: Ejemplo del plano cartesiado mostrando en rojo la correspondencia de valores para $y(x) = x^2$, donde los puntos corresponden a los pares de valores $(x = -1, y = 1), (-0.5, 0.25), (0, 0), (0.5, 0.25), (1, 1)$.

La función matemática más sencilla que puede describir esta forma en el plano cartesiano es:

\[\begin{equation} y(x) = x^2 \end{equation}\]

Al igual que con los modelos lineales, las parábolas pueden representarse matemáticamente de otras formas más complejas:

$y(x) = a + bx + cx^2$
$y(x) = a + cx^2$
$y(x) = -x^2$

Si uno es observador, se dará cuenta de que estas ecuaciones son muy similares a la recta, y es que es posible considerar que $x^2$ se puede considerar como otro conjunto tal que $x' = x^2$, resultando así en funciones perferctamente lineales:

$y(x) = a + bx + cx'$
$y(x) = a + cx'$
$y(x) = -x'$

Entonce, lo que realmente distingue matemáticamente a una parábola de una recta, es la doble ocurrencia de cada valor de $y$ para los distintos valores de $x$:

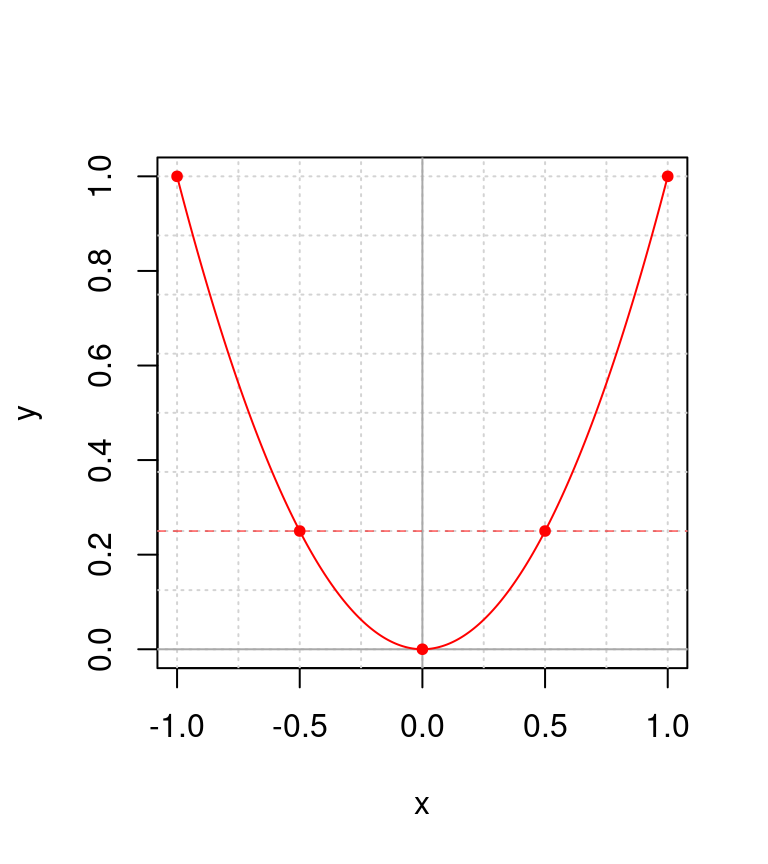
Figura 4.4: Correspondencia de dos valores distintos de $x$ para el mismo valor de $y$

Cuando esto ocurre, las funciones tiene un solo punto a lo largo de todos los valores de $x$, donde sólo va a ocurrir un valor único de $y$. A estos puntos se les conocen como mínimos (par de valores con coordenadas $(0, 0)$ en la figura 4.4). Los máximos, en cambio están ilustrados en la figura 4.5, e igual corresponde al punto con coordenadas $(0, 0)$.

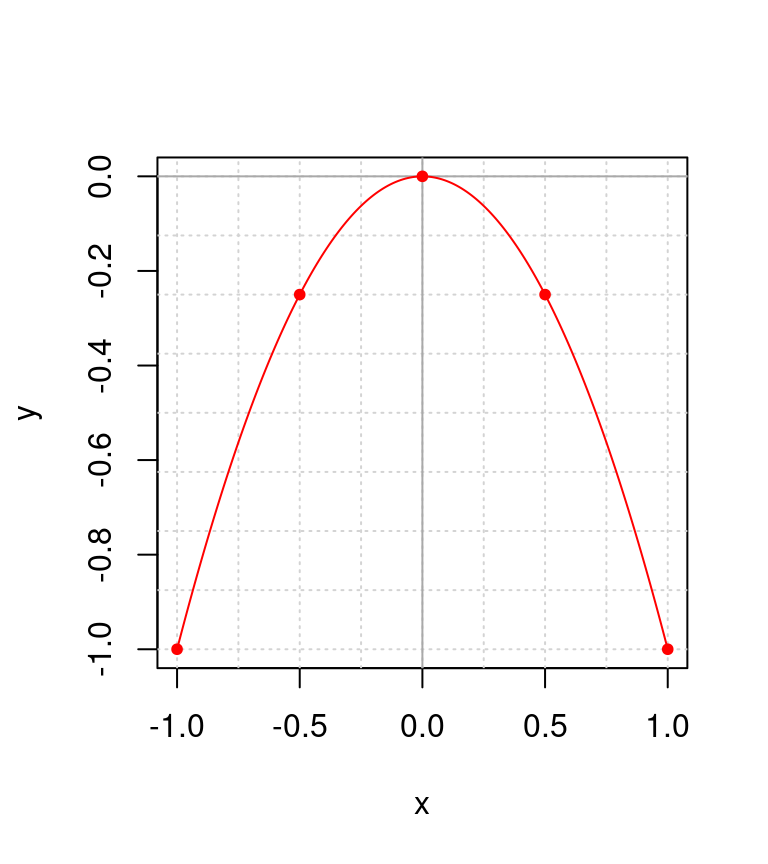
Figura 4.5: Correspondencia de valores para $y = -x^2$.

En los modelos parabólicos más sencillos ($y(x) = x^2, y(x) = -x^2$), los puntos mínimos y máximos siempre estarán en las coordenadas $(x = 0, y = 0)$, pero es posible alterarlos. Por ejemplo en $y(x) = 2 + x^2$, el mínimo estará en $(x = 0, y = 2)$. Para verificarlo resuelve $y(x) = 2 + x^2$ para $y(0)$, sustituyendo $x$ por $0$.

4.2.0.1 Ejercicio

A estas alturas, ya te podrás haber dado cuenta de ciertas propiedades de las parábolas, contesta las siguientes preguntas:

¿Qué tipo de punto único (mínimo o máximo) habrá en las siguientes parábolas?

1.1. $y(x) = 2 - x^2$ 1.2. $y(x) = 2x - 2x^2$ 1.3. $y(x) = 1 - x + 3x^2$ 1.4. $y(x) = x/2 - 4x^2/x$ 1.5. $y(x) = (5x)^2 - 3x + 1$

4.3 Cónicas

De manera muy general, una cónica es el conjunto de soluciones para una ecuación cuadrática cuando menos en dos variables. Por lo tanto, las parábolas, vistas en la sección anterior, son un tipo de cónica. Geométricamente las cónicas surgen a partir de la intersección entre un plano y dos conos tridimensionales superpuestos en sus vértices.

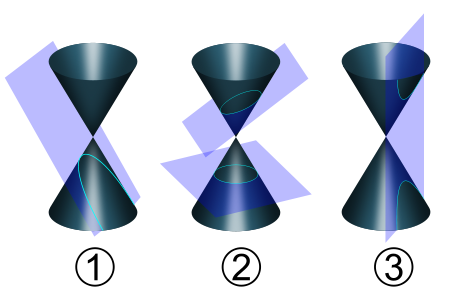
Las diferentes formas geométricas generadas por las cónicas pueden ser descritas algebráicamente por las siquiente expresiones (figura 4.6):

$x^2 + y^2 = -1$
$x^2 + y^2 = 0$
$x^2 - y^2 = 0$
$xy - 1 = 0$
$x^2 - y = 0$

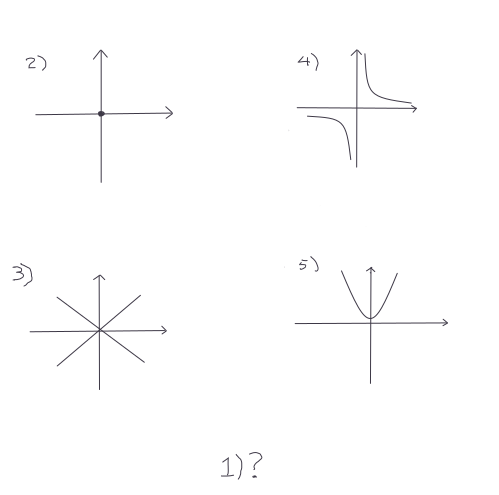
Figura 4.6: Representación gráfica de las ecuaciones 1-5.

4.4 La curva normal

En el curso de probabilidad y estadística, se acordarán, se mencionó repetidamente a la distribución normal. En cuestión de matemáticas, la distribución normal puede ser representada como una ecuación:

\[\begin{equation} y(x) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \tag{4.1} \end{equation}\]

donde $\mu$ es la media aritmética, $\sigma^2$ es la varianza y $x$ son todos los valores de la variable que observamos. Cuando tenemos datos de un experimento y los analizamos haciendo el cálculo del promedio estimamos justamente a $\mu$ de la ecuación (4.1), y al estimar la varianza obtenemos a $\sigma^2$ de la misma ecuación. Como es importante notar, al hacer estos cálculos estamos asumiendo que nuestros datos tienen una distribución (un histograma) que puede ser descrita por la ecuación (4.1).

Como vimos en la sección de parábolas, las funciones que no son monótonas (los valores de $y$ no aumentan o disminuyen a lo largo de $x$), tienen un punto máximo o mínimo. La curva normal, tiene propiedades similares, aunque debido a la presencia de la función exponencial ($e^{\dots}$), los valores de $y(x)$ siempre serán positivos. Por lo tanto, la curva normal tiene un punto máximo que corresponde a $y(\mu)$, o sea, $y$ alcanza su punto máximo cuando $x=\mu$ (Figura 4.7).

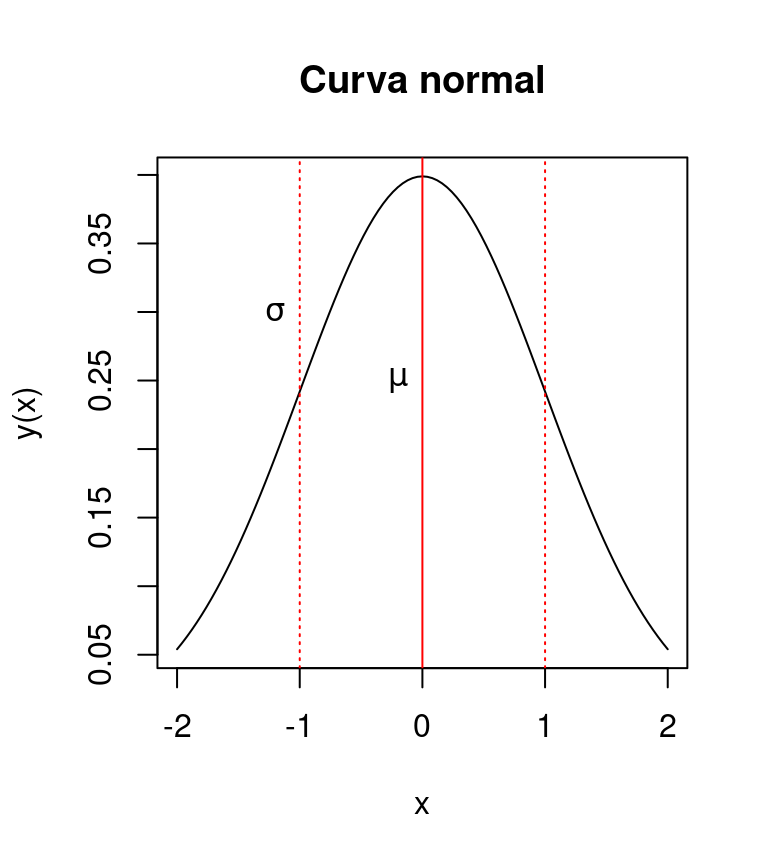
Figura 4.7: Representación gráfica de la curva normal.

En estadística, esta función representa en el eje de las $y$ la densidad de la variable $x$. Densidad se refiere a la proporción de observaciones de $x$ dentro de un intervalo definido de $x$. Por lo tanto, la curva normal, representa la probabilidad de observar ese valor de $x$, de ahí que $\mu$ sea el valor teórico más probable. En lo que respecta a $\sigma^2$, éste representa qué tan concentrados estarán los valores de $x$ alrededor de $\mu$. Altos valores de $\sigma$ se traducirán en baja concentración alrededor de $\mu$ (Figura 4.8).

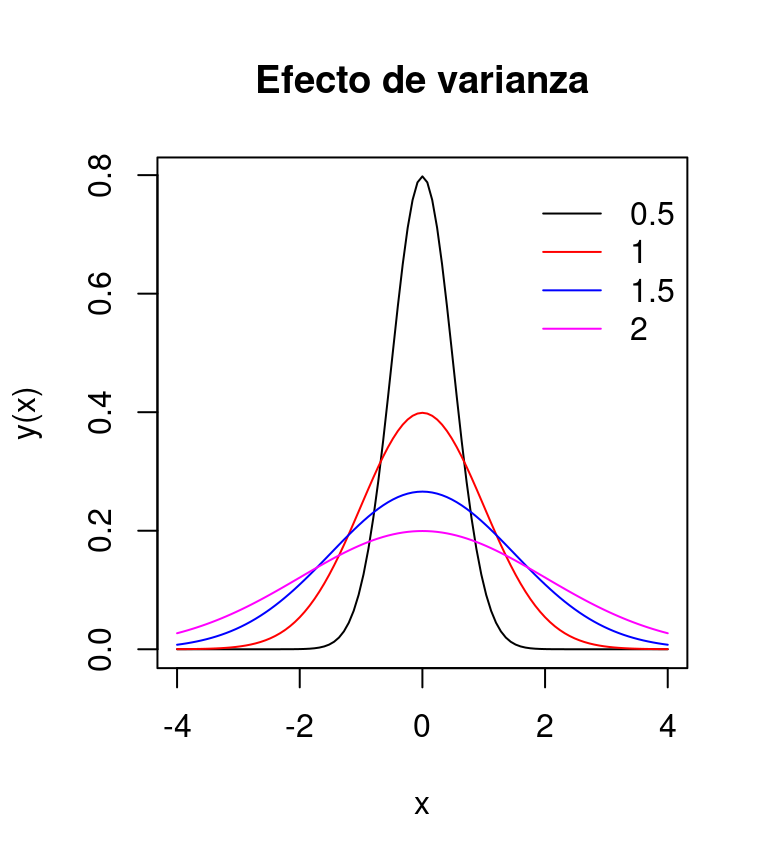
Figura 4.8: Efecto de la varianza sobre la la dispersión alrededor de la media.

4.5 Funciones trigonométricas

En esta sección revisaremos algunas de las funciones trigonométricas y cómo se representan en el plano cartesiano.

La trigonometría es una rama de las matemáticas que se comenzó a desarrollar a partir de la necesidad de medir distancias de manera indirecta. Por ejemplo, la distancia entre la luna y la tierra y la tierra y el sol, la distancia entre dos barcos, la distancia entre un barco y el puero más cercano. Las herramientas trigonométricas entonces se comenzaron a desarrollar utilizando la geometría de triángulos rectángulos. Aquí es preciso describir el teorema de los triángulos proporcionales, dados dos triángulos con ángulos internos idénticos y longitudes de lados diferentes, los cocientes de las longitudes de sus lados serán iguales (Figura 4.9).

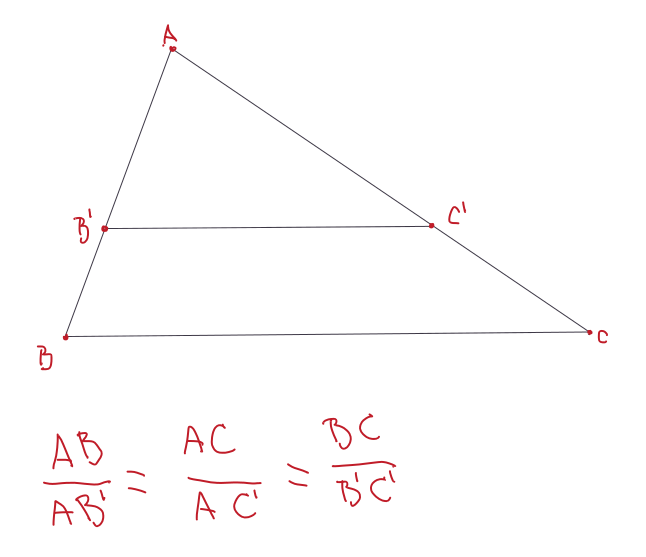
Figura 4.9: El teorema de los ángulos proporcionales es la base para las fórmulas geométricas de las funciones trigonométricas.

De modo que sin importar las longitudes de los lados, los cocientes de las longitudes siempre serán iguales, lo cual se puede extender a todos los triángulos rectángulos, la base geométrica para la trigonometría. Aquí veremos entonces las funciones trognométricas básicas seno, coseno y tangente.

4.5.0.1 Nomenclatura de triángulos para trigonometría básica

Hay una serie de términos tradicionales que se emplean en trigonometría, los cuales utilizaremos a lo largo del curso. Se trata de los nombres que se dan a los lados y ángulos internos de un triángulo rectángulo. Por lo general, el triángulo rectángulo lo interpretaremos como una representación del plano cartesiano, de modo que los catetos corresponden a los ejes de las $x$ y $y$, y son los lados que forman un ángulo recto al cruzarse. El lado que los une en secante, es la hipotenusa. El ángulo que forma la hipotenusa con el eje de las $x$ tradicionalmente recibe el nombre con la letra griega $\theta$ (teta).

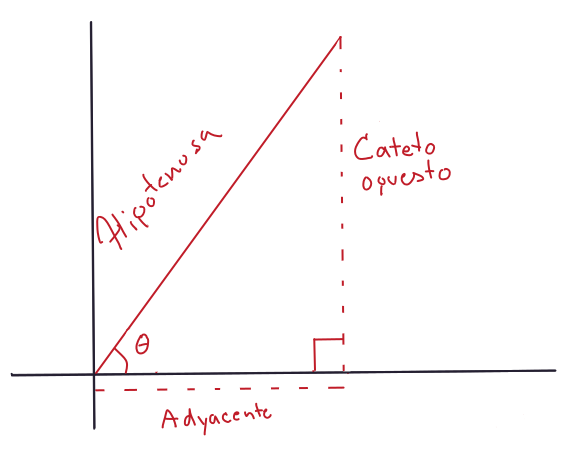
Figura 4.10: Representación gráfica de las partes del triángulo y los nombres que reciben tradicionalmente en trigonometría plana.

4.5.0.2 Las funciones trigonométricas básicas

Todas las funciones trigonométricas representan una descripción del ángulo $\theta$ como el cociente de la longitud de dos lados del triángulo rectángulo de modo que:

Seno: $\sin(\theta) = \frac{\mathrm{Opuesto}}{\mathrm{Hipotenusa}}$
Coseno: $\cos(\theta) = \frac{\mathrm{Adyacente}}{\mathrm{Hipotenusa}}$
Tangente: $\tan(\theta) = \frac{\mathrm{Opuesto}}{\mathrm{Adyacente}}$

Para recordar las fórmulas de cada función podemos utilizar la mnemotecnia:

Seno: SOH (Seno, Opuesto, Hipotenusa)
Coseno: CAH (Coseno, Adyacente, Hipotenusa)
Tangente: TOA (Tangente, Opuesto, Adyacente)

4.5.0.3 Representación gráfica de las funciones trigonométricas

Para entender por qué las funciones trigonométricas se comportan como lo hacen es útil tener en cuenta que representan el cociente de dos números que cambian uno en relación del otro. Esto queda de manifiesto en la Figura 4.11. Como se puede apreciar, la hipotenusa ($H$ en la misma figura) se mantiene constante, pues representa el radio de la circunferencia, mientras que los catetos se alargan o encojen conforme la hipotenusa se acerca a los ejes $x$ o $y$.

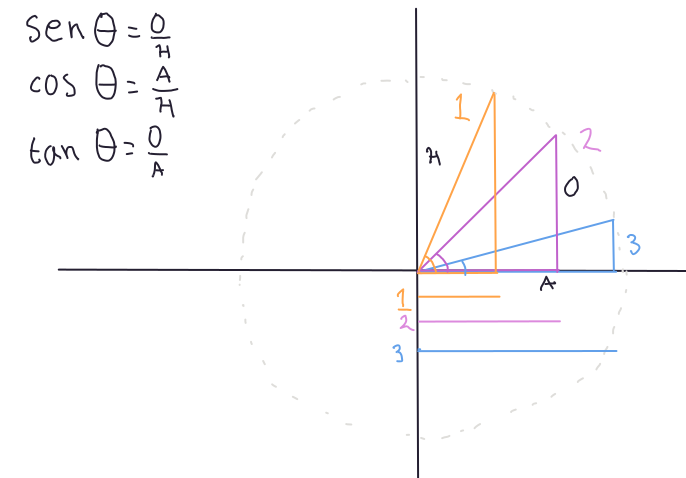
Figura 4.11: Representación gráfica del efecto del ángulo sobre la longitud de los catetos.

Como es de esperarse, los valores del seno y coseno están limitados por 1 y -1 cuando la longitud del cateto es igual a la hipotenusa. La tangente, por otro lado, puede tomar valores que van de $-\infty, +\infty$ cuando el cateto adyacente tiene longitud cero $0$. Aquí, mediremos los ángulos en radianes, o unidades de $\pi$, donde $\pi = 180°$

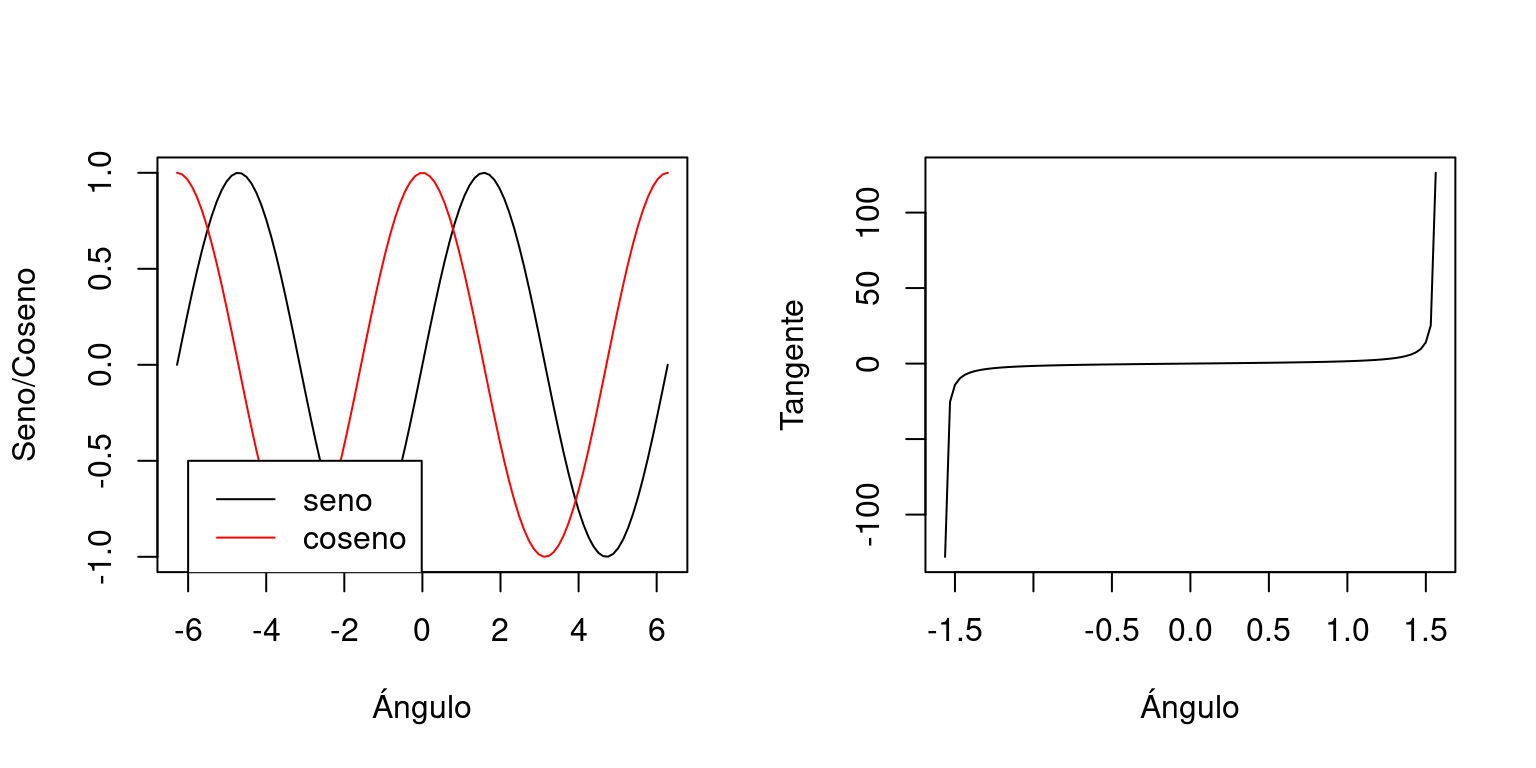
Figura 4.12: Gráfica de las funciones trigonométricas básicas.

Las funciones seno, coseno y tangente son las básicas en trigonometría. Otras funciones comunes, pasadas en la inversión de las mecionadas son la secante, cosecante y cotangente respectivamente. Al igual que otras operaciones aritméticas, para las funciones trigonométricas, existen inversiones. La inversión de una multiplicación es una divisón, de la suma es la resta, del exponente es la raíz. Las inversiones de las funciones trigonométricas reciben el nombre de Arco-$f(\theta)$, de modo que al aplicarlas al resultado de la función obtenemos el valor del ángulo:

$\theta = \arcsin \left(\frac{0}{H}\right)$
$\theta = \arccos \left(\frac{A}{H}\right)$
$\theta = \arctan \left(\frac{O}{A} \right)$

4.5.0.4 Aplicaciones de las funciones trigonométricas

En mi experiencia, las dos funciones con más aplicaciones en modelación de sistemas ambientales son la tangente y el coseno. Para comenzar, la tangente de un ángulo tiene una relación directa con la pendiente de una recta. Si recordamos la recta está descrita por la ecuación:

\[\begin{equation} y = a + bx \tag{4.2} \end{equation}\]

donde $b$ es la pendiente de la recta que se forma al graficar $x$ y $y$ en el plano cartesiano. En realidad $b$ es la tangente del ánguo que se forma entre la recta y el eje de las $x$. Por lo tanto, cuando nos encontramos ante un modelo formulado por medio de ecuaciones diferenciales, por ejemplo, lo valores que obtenemos al hacer los cálculos de ese sistema es una pendiente o tangente.

El coseno, por otro lado, nos es muy útil para forzar la oscilación de algún parámetro. Ello es necesario cuando estamos interesados en representar fenómenos cíclicos como la temperatura diaria o anual. En la práctica, podemos reemplazar la pendiente $b$ de la ecuación (4.2) por una función coseno.

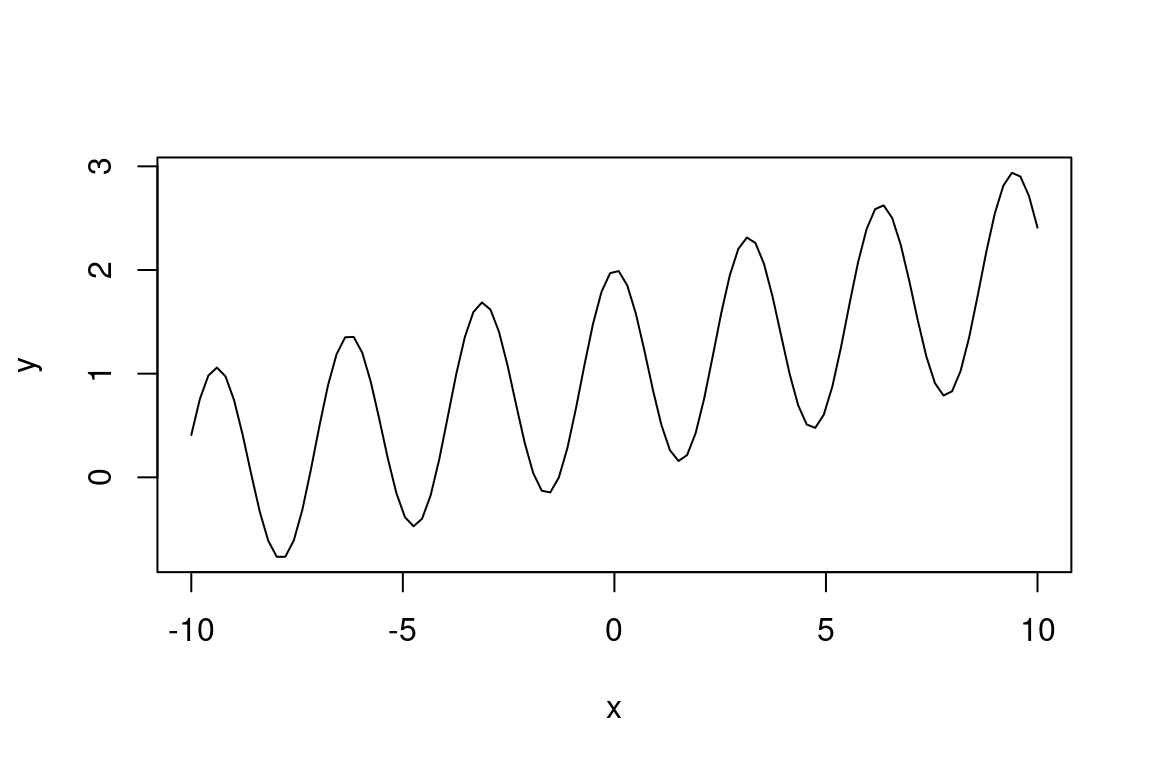
Figura 4.13: Gráfica de la función $y = 2 cos(x)^2 + 0.1 x$.

4.6 La recta como modelo “universal” y sus transformaciones

De los modelos vistos anteriormente, la línea recta es el más flexible y común de todos. Por su simplicidad, puede ser utilizado para representar muchos fenómenos de la naturaleza, incluso aquellos cuyo comportamiento es… !no lineal¡

Cuando decimos no lineal, nos referimos, generalmente, a los casos en que una regla de correspondencia entre $x$ y $y$ representada en el plano cartesiano no forman una línea recta. Ya hemos visto que, matemáticamente, es posible concebir como lineales reglas de corresondencia que geométricamente no son lineales, de ahí que la línea recta sea tan flexible. Para que una ecuación sea considerada como lineal debe cumplir con las siguientes características:

Sólo hay adición de variables
Sólo hay multiplicación con constantes
Las variables solo están elevadas a la potencia 1

Con base en estas definiciones, las siguientes ecuaciones no son lineales

$xy = 1$
$y = a + b x^2$
$y = e^x$

Aún cuando estas expresiones no son lineales, es posible transformar algunas de ellas para que adquieran propiedades lineales. Para comenzar, el caso 1, no puede ser linealizado. Para el caso 2, ya vimos un transformación posible, si asumimos que existe una $x'$ tal que $x' = x^2$. Para el caso 3 hay que usar un poco más de conocimiento de dos funciones matemáticas, el logaritmo y la exponencial.

4.6.1 El logaritmo

Para entender cómo funciona la transformación logarítmica, revisemos qué hace el logaritmo. Supongamos que queremos encontrar el valor de la incógnita $x$ en la siguiente ecuación:

\[10^x = 20\] La operación necesaria para invertir el radical $10^x$ y encontrar el valor de $x$ es precisamente el logaritmo base 10, de modo que:

\[\log_{10} 10^x = \log_{10} 20\] \[x \log_{10} 10 = \log_{10} 20\] sabemos que $\log_{10} 10 = 1$ pues $10^1 = 10$ por lo que:

\[x = \log_{10} 20 \approx 1.3\] Así como en esta ocasión utilizamos $\log_{10}$ (logaritmo base 10), se puede utilizar como base cualquier número $b > 0$, si está en el conjunto de los números reales (positivos). El logaritmo más común recibe el nombre de natural, que utiliza de base la constante $e = 2.718282 ...$ de Euler. La convención en escritura de logaritmos es:

Logaritmo natural: $\ln$
Logaritmo base 10: $\log$
Logaritmo base $b > 0, b \in \mathbb{R}$: $\log_b$

Aún cuando esta es la convención más común, en la modelación, la mayoría de las veces que se utiliza $\log$ se refiere a $\ln$, de modo que a menos que se especifique la base, $\log$ y $\ln$ también significan $\log_e$.

4.6.2 La función exponencial

Una de las funciones más comunes en aplicaciones matemáticas es la exponencial que se denota por $\exp(x)$, que significa $e^x$. De este modo cuando $y$ es una función exponencial de $x$, tenemos que:

\[y(x) = \exp(x) = e^x\] La función exponencial puede tomar formas más complejas, por ejemplo, conteniendo una ecuación lineal:

\[y(x) = \exp(a + bx) = e^{a + bx}\] y dadas las reglas de los exponentes, también es equivalente a:

\[y(x) = e^a e^{bx} = a' e^{bx}\]

4.6.2.1 Linealizando la función exponencial

Como se ha mostrado en esta sección, transformar una función exponencial en lineal es relativamente sencillo. En sentido literal, las transformaciones logaritmicas no son lineales sino log-lineales pues:

\[\begin{equation} y(x) = e^{a + bx} \tag{4.3} \end{equation}\]

se convierte en:

\[\begin{equation} \log y(x) = a + bx \tag{4.4} \end{equation}\]

donde el lado izquierdo es una función logarítmica y el derecho es estrictamente lineal. Matemáticamente entonces, la transformación es lineal $\forall x \in \mathbb{R}$, puesto que $\log y$ puede tomar cualquier valor entre $-\infty$ y $+\infty$. Entonces, la ecuación número 3 de la lista de ecuaciones no-lineales al principio de esta sección es:

\[\log y(x) = \ln y(x) = x\]

Esta equivalencia, como veremos más adelante y como verán en modelación estadística, es sumamente útil en la modelación de sistemas dinámicos.

4.6.2.2 Representación gráfica de la función exponencial

En la función exponencial, la variable $y$ crece muy rápido. De hecho, su crecimiento en cualquier punto es proporcional al valor que tiene en ese punto. Es decir que si tomamos un punto cualquiera en $y$ y dibujamos una tangente a ese punto, la pendiente de esa recta tendrá el mismo valor que $y$.

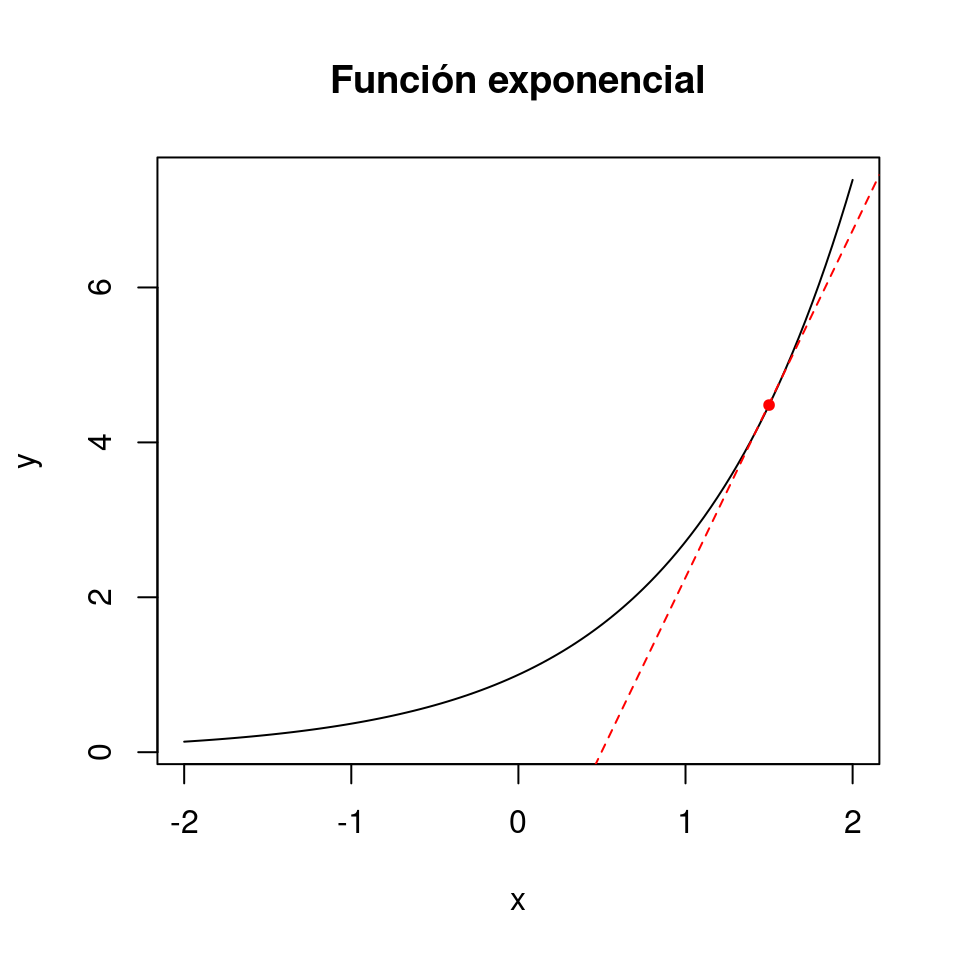
Representación gráfica de la función exponencial. El punto rojo representa y = exp(1.5), de modo que la pendiente de la recta tangente a la curva (en rojo) en ese punto es precisamente exp(1.5).

Figura 4.14: Representación gráfica de la función exponencial. El punto rojo representa y = exp(1.5), de modo que la pendiente de la recta tangente a la curva (en rojo) en ese punto es precisamente exp(1.5).

Esta relación entre el valor de la curva y la pendiente tiene implicaciones importantísimas en modelación de poblaciones, pues expone las razones por las cuales el crecimiento demográfico puede ser descrito como exponencial: el crecimiento neto de una población, el total de individuos nuevos que se incorporarán a la población, en ese instante es proporcional al número de individuos repoductivos de esa población. Es por esta razón que el número total de individuos que nacen en una población es más grande cuantos más individuos haya, a pesar de que la tasa reproductiva por unidad de tiempo sea la misma.

Veamos como ejemplo, que el crecimiento de la humanidad, desde que se pueden obtener estimaciones, es aproximadamente exponencial 4.15.

Población humana a lo largo del tiempo, según estimaciones de [Our world in data](https://ourworldindata.org/world-population-growth).

Figura 4.15: Población humana a lo largo del tiempo, según estimaciones de Our world in data.

A diferencia del ejemplo de la figura 4.14, donde $y = \exp(x)$, para representar el crecimiento de la población humana tenemos que medir la tasa reproductiva, de modo que podamos establecer la relación directa entre el tiempo y el tamaño de la población. En otras palabras, medir cuántos individuos son producidos en promedio por cada individuo presente en la población en cada unidad de tiempo:

\[\begin{equation} N(t) = \exp(r \cdot t) \tag{4.5} \end{equation}\]

donde $r$ es la tasa reproductiva de la población y utilizamos $N$ en lugar de $y$ para representar al $N$úmero de individuos, y $t$ en lugar de $x$ para dejar claro que $x$ representa tiempo. Si utilizamos el conocimiento de la subsección anterior, veremos que al aplicar el logaritmo a ambos lados de la ecuación (4.5) obtenemos ¡una ecuación lineal!

\[\begin{equation} \log N = r \cdot t \end{equation}\]

Es evidente que un modelo tan sencillo como este tiene serias deficiencias biológicas. Por ejemplo, cuando $t = 0$, $\exp(r \cdot t) = 1$, de modo que se asume que siempre habrá cuando menos un individuo presente. Esto puede o no ser cierto, por lo que una forma más generalizable incluye un intercepto para el tamaño poblacional inicial:

\[\begin{equation} N(t) = N_0 e^{r \cdot t} \rightarrow \log N(t) = \log N_0 + r \cdot t \end{equation}\]

4.6.2.3 Representación gráfica del logaritmo

A diferencia de la función exponencial, donde el crecimiento de $y$ es cada vez más rápido, en el logaritmo es más lento (figura 4.16).

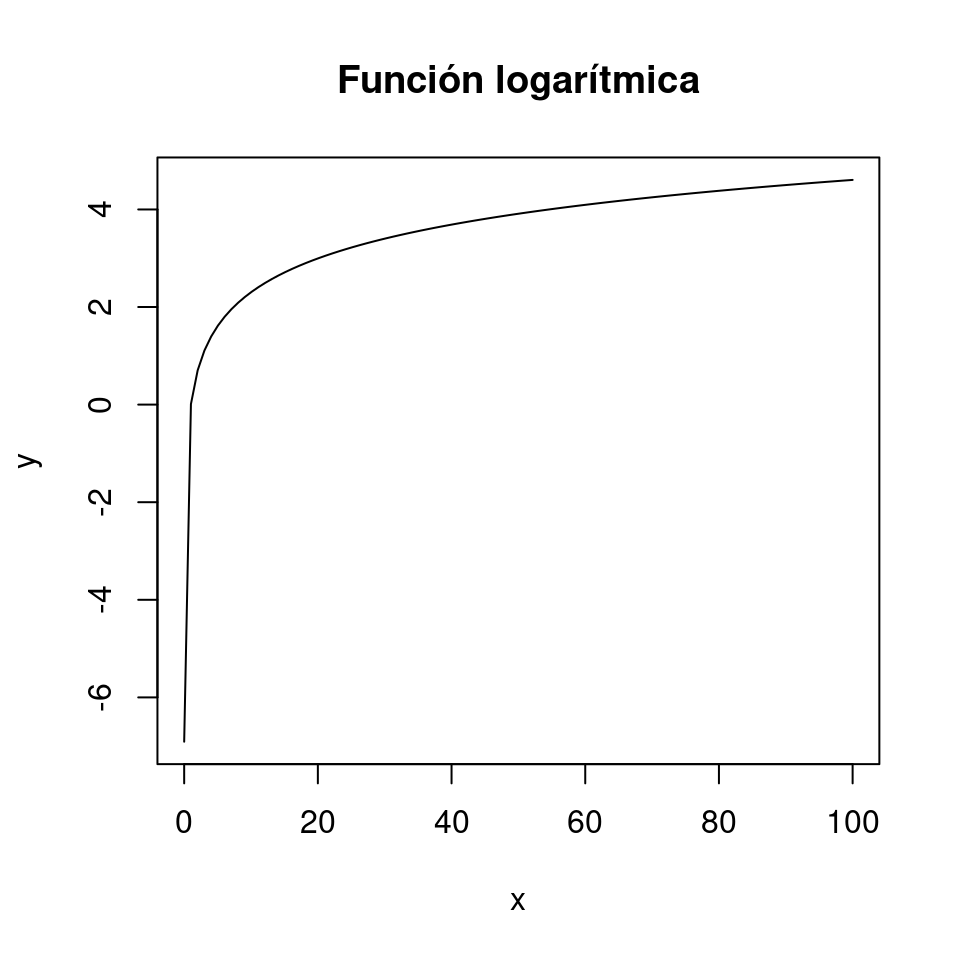
Figura 4.16: Representación gráfica del logaritmo con y = log x.

4.6.3 Relevancia de la recta

Una vez cubiertas las funciones logarítmicas y exponenciales, hemos comenzado a vislumbrar la relevancia más amplia de la recta para fenómenos que no son lineales. En el cálculo diferencial, la recta nos da los elementos para entender el significado de la derivada, y también es el bloque fundamental para implementar métodos de integración numérica relativamente sencillos, para ecuaciones diferenciales que no se pueden integrar analíticamente.

4.7 Representación de las funciones en 3 dimensiones

Hasta ahora sólo hemos visto funciones de dos variables, y su representación en el plano cartesiano. Las funciones de tres variables, requieren ser representadas en 3d. Puesto que hay tres dimensiones, pueden ser confusas. Para comenzar, al conveción para funciones de tres variables es que hay dos dominios llamados $x$ y $y$, y un solo codominio llamado $z$, por lo que $z$ es una función $z(x, y)$. La gráfica de estas funciones, pueden ser en efecto sólo una línea en el epacio, o un plano, o algo mucho más complejo. Para representar un plano, necesitamos una ecuación lineal como

\[z(x, y) = x + y\] y hacer los cálculos de $z$ para todas las combinaciones posibles de $x$ y $y$, por ejemplo:

(#tab:tabla.xy)Todas las combinaciones posibles de (x, y) y el valor resultante de z.
x	y	z
0	0	0
1	0	1
2	0	2
3	0	3
0	1	1
1	1	2
2	1	3
3	1	4
0	2	2
1	2	3
2	2	4
3	2	5
0	3	3
1	3	4
2	3	5
3	3	6

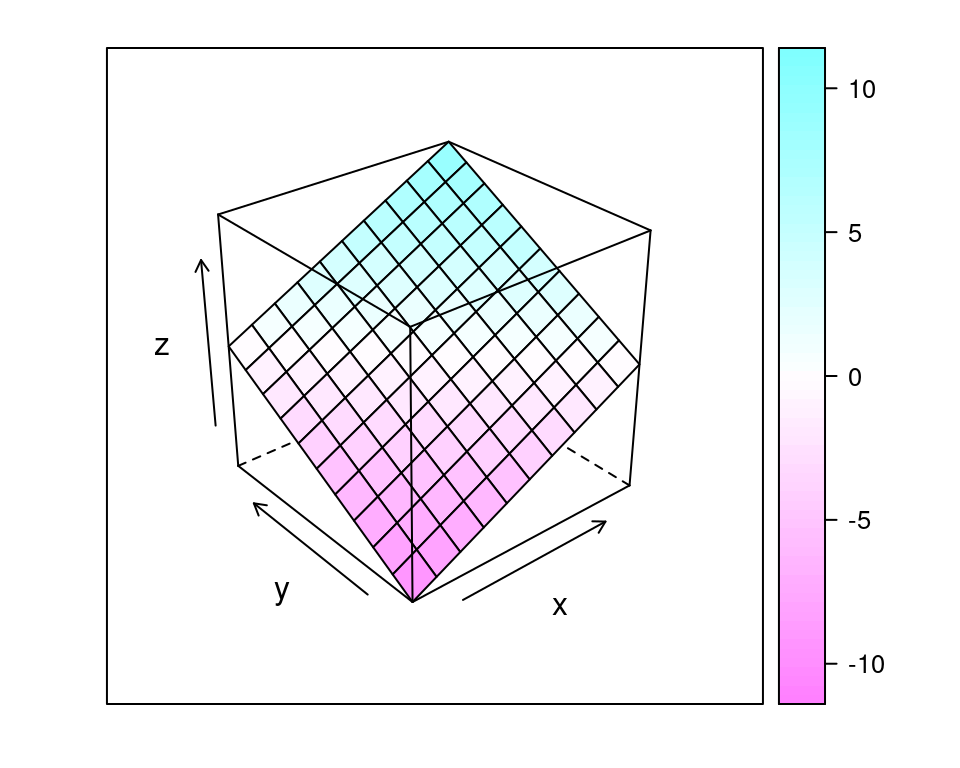
Figura 4.17: Representación gráfica de la función $z(x, y) = x + y$.

Para poder hacer esta gráfica, es necesario hacer los cáculos para todas las combinaciones posibles de $x$ y $y$, de modo que conocemos todos los valores posibles de $z$ para cada par de valores del dominio. Si en la representación en dos dimensiones, necesitamos $n$ valores, en la representación 3d necesitamos $2 \times n^2$, lo cual produce $n^2$ diferentes valores de $z$.

Las funciones trigonométricas pueden representarse

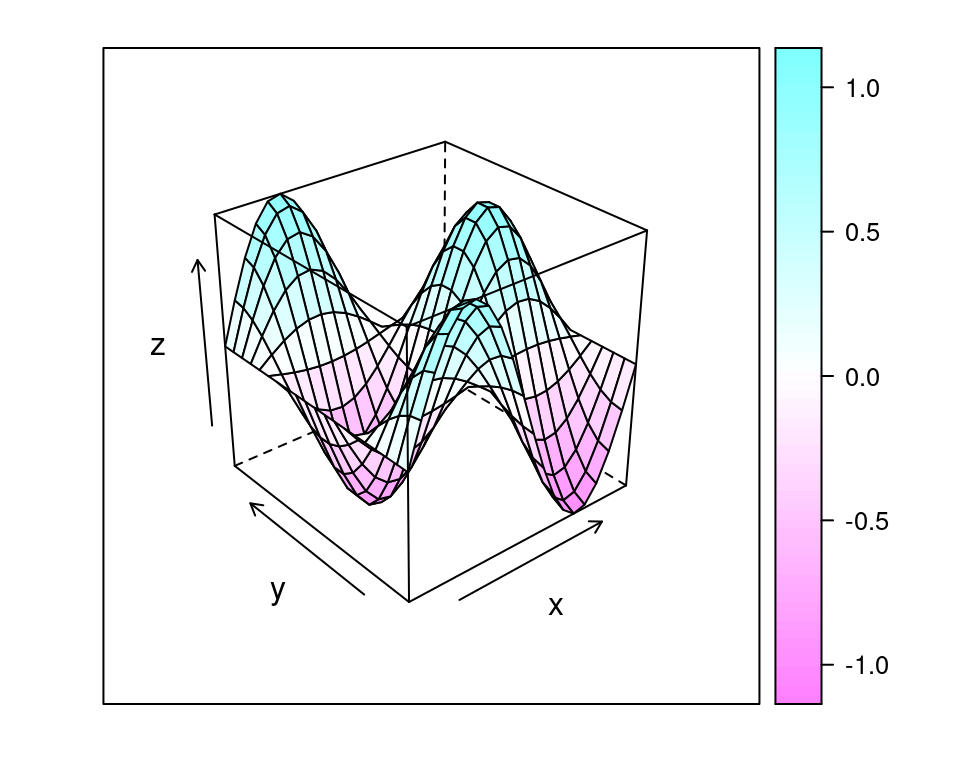
Figura 4.18: Representación en 3d de la función trigonométrica $z(x, y) = cos(x) sin(y)$.