3 Unidad I: Introducción a la modelación

3.1 Introducción al concepto de modelo matemático

Para comenzar a hablar de modelos matemáticos es preciso tener una idea de por qué las matemáticas forman parte de un grado en ciencias naturales. Los autores Otto and Day (2011), dan cuenta de qué tan comunes son las matemáticas en la labor del biólogo/ecólogo. Hacia el año 2006, una búsqueda sistemática del material publicado en revistas científicas contentiendo la palabra clave “math” sugiere que había ~900 mil artículos, la mayoría concentrados en revistas especializadas como Bulletin of Mathematical Biology, otros en las más prestigiosas Nature o Science. Una mirada más cercana a las revistas especializadas Ecology and Evolution y American Naturalist que el 35 y 60% respectivametne de las publicaciones utilizaron algún modelo matemático para mostrar predicciones. En resumen, la labor de un ecólogo requiere del uso frecuente de matemáticas, si no es mediante el desarrollo de algún modelo, requiere de su entendimiento.

3.1.1 ¿Qué es un modelo?

Imaginemos a seis personas invidentes, con la tarea de encontrar qué es el objeto que está frente a ellas usando únicamente el tacto. En la parábola de los seis hombres ciegos, el objeto es un elefante, de modo que la imágen que cada uno de ellos se forma del objeto depende enteramente de la parte del elefante que están tocando.

Figura 3.1: La parábola de los seis hombres ciegos inspeccionando un elefante.

Quien toque los colmillos podrá pensar que se trata de una lanza, la trompa podría tratarse de una serpiente, la cola de una cuerda, las patas troncos de árbol y el cuerpo una pared. Es evidente que todas las hipótesis presentadas después de la inspección fueron erróneas, y que cuando estudiamos al mundo lo haremos igual, con la descripción de tan sólo una fracción de éste. Un séptimo hombre que pregunte a los otros seis qué fue lo que vieron podría formarse una imágen más completa del sistema para proponer otra hipótesis: se trata de un objeto grande reposando sobre cuatro columnas con apéndices adelante y atrás.

Al estudiar los sistemas ecológicos, al igual que los ciegos, no sabremos que estamos frente a un elefante. Los sistemas ecológicos, al igual que los elefantes, también tienen componentes interconectados, y nosotros los ecólogos somos como los hombres ciegos, sólo podemos observar ciertas partes de los ecosistemas. En nuestro trabajo entonces, aprender a identificar y proponer hipótesis sobre cómo funcionan los sistemas ecológicos.

Las hipótesis propuestas por los seis hombres representan modelos, es decir simplificaciones del mundo que nos ayudan a entenderlo. Los modelos matemáticos son simplificaciones formales del mundo utilizando otro lenguaje, las matemáticas (Haefner 1998).

3.2 Cómo construir un modelo

¿Cómo se construye un modelo? Es una pregunta difícil de responder, pues difícilmente existe un sólo modo de hacerlo que funcione para tod@s. Aquí voy a hablar de mi propia experiencia, y cómo aprendí a utilizar las matemáticas y estadística para entender los sistemas ecológicos. Los pasos generales que sigo son:

1. Identificar el sistema y sus componentes
2. Crear un modelo conceptual, haciendo dibujos
3. Identificar las herramientas matemáticas disponibles para representar el modelo conceptual
4. Establecer objetivos claros y alcanzables
5. Proponer una serie de modelos alternativos
6. Determinar una estrategia para seleccionar uno solo de los modelos que propuse para logar el objetivo

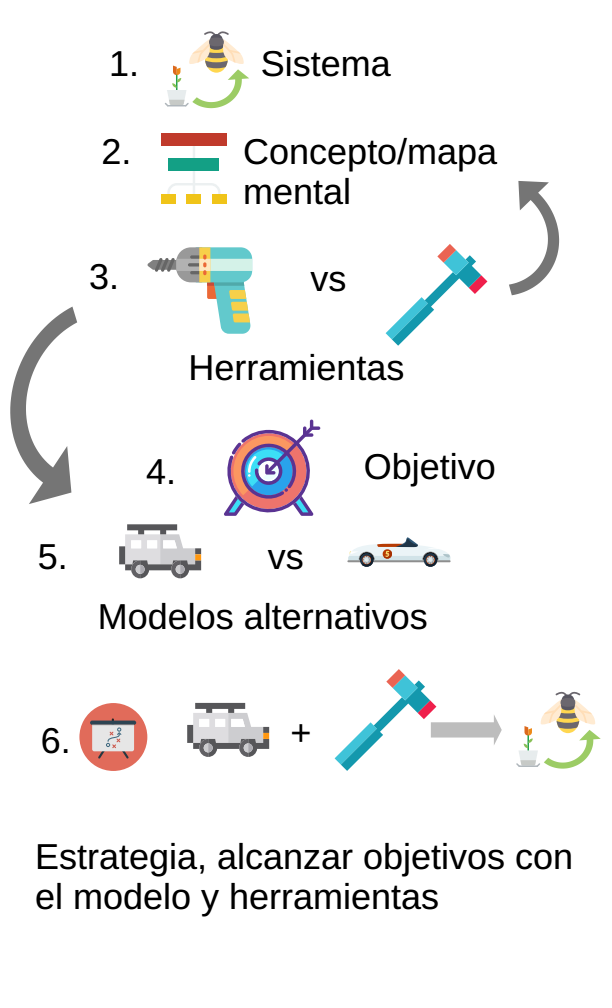
Figura 3.2: Diagrama de mi estrategia para desarrollar modelos.

La estrategia general que les doy puede, por el momento, sonar un tanto abstracta, pero la iremos poniendo en práctica conforme avanza el curso para que al final, esperemos, tenga más sentido que ahorita.

3.2.1 Ejemplos

La presente pandemia ha puesto en boca de todxs muchos aspectos de la modelación matemática y estadística. Como es de esperarse, los modelos son distintos dependiendo del objetido que se quiera conseguir con ellos:

1. Determinar el número reproductivo básico (\(R_0\)) de COVID-19
2. Predecir la ocupación hospitalaria ante ciertas medidas de restricción de movilidad
3. Estimar cómo cambiaría el número reproductivo básico ante ciertas medidas de restricción
4. Predecir localidades geográficas donde surgirán nuevas cepas
5. Predecir las cualidades infecciosas o virulentas de las nuevas cepas

Todos estos objetivos puede de cierta manera conseguirse por medio de modelos matemáticos, todos ellos con modelos muy distintos, algunos con herramientas muy diferentes unos de otros.

3.3 Discusión sobre las distintas herramientas matemáticas empleadas en la modelación matemática

Las matemáticas son un área de conocimiento muy extenso, por lo que hablar de todas las herramientas disponibles ¡nos podría llevar años! En este curso nos vamos a enfocar en un tipo general de modelo y de sistema ecológico: aquellos que cambian rápidamente con el tiempo, también llamados dinámicos.

Las herramientas matemáticas más comunmente utilizadas para estudiar estos sistemas son las ecuaciones diferenciales ordinarias, ecuaciones por diferencias finitas y el álgebra de matrices. Las ecuaciones diferenciales y por diferencias finitas son muy parecidas entre sí, porque nos representar y medir los cambios que sufre un sistema ecológico a través del tiempo en cada uno de sus componentes. Además es fácil representar las ideas plasmadas diagramáticamente en ellas. El álgebra de matrices, por otro lado, nos sirve para conectar los cambios de los diferentes componentes del sistema de estudio, y así hacer cálculos sobre sus cambios como un todo. Por supuesto que para poder utilizar las matrices de este modo, tenemos que echar mano de una serie de supuestos de linealidad, de modo que el álgebra lineal también es una herramienta básica.

Como podemos ver, gran parte de este curso estará enfocado en entender y medir los cambios. Te preguntarás entonces ¿cambios de qué? En ecología, estos son algunos de los cambios que nos interesa observar:

1. Número de individuos de una especie
2. Cantidad de materia orgánica almacenada en la vegetación
3. Calorías consumidas por una población de aves
4. Probabilidad de extinción de una especie

Cuando medimos cambios entonces, es necesario observar el estado del mundo natural en diferentes puntos a lo largo del tiempo. Por lo tanto, la modelación matemática también requiere desarrollar buenas habilidades estadísticas. Estas últimas nos permitirán entender probabilísticamente a los sistemas ecológicos a partir de los mecanismos que representamos en los modelos matemáticos. Más adelante veremos a qué nos referimos con probabilísticamente.

Antes de entrar en estos temas más filosóficos, sin embargo, debemos que conocer algunas expresiones algebráicas y geométricas que utilizaremos rutinariamente para representar fenómenos. Algunas de las expresiones y herramientas geométricas más comunes son:

1. La recta, descrita por expresiones como \(y = a + bx\)
2. La parábola, \(y = x^2\)
3. Las Cónicas, \(y = 1/x\), o \(y^2 - x^2 = 1\) y muchas otras
4. Las funciones trigonométricas, \(\sin \theta = \frac{O}{H}\)

Estas expresiones pueden ser combinadas dentro de un sistema de ecuaciones. Con sistema de ecuaciones nos referimos a ecuaciones separadas que están conectadas por términos en común y que representan flujos. Veamos un sencillo sistema de ecuaciones estructuradas por edad con crecimiento logístico:

\[\begin{equation} \dot{J} = rA - \gamma A^2 - \kappa J \tag{3.1} \end{equation}\]

\[\begin{equation} \dot{A} = \kappa J \tag{3.2} \end{equation}\]

La expresión \(rA - \gamma A^2\) es claramente una parábola, y representa el crecimiento logístico. Por otra parte \(- \kappa J\) es un término lineal que, debido a su signo negativo representa un flujo de salida del compartimento \(J\) y es una entrada al compartimento \(A\). Este modelo relativamente sencillo representa la dinámica poblacional de un bicho con estados de desarrollo juvenil \(J\) y adulto \(A\), donde el nacimiento de individuos juveniles depende el número de adultos, y el crecimiento de los adultos ocurre a medida que los juveniles maduran y entran al compartimento de adultos a una tasa \(\kappa\).

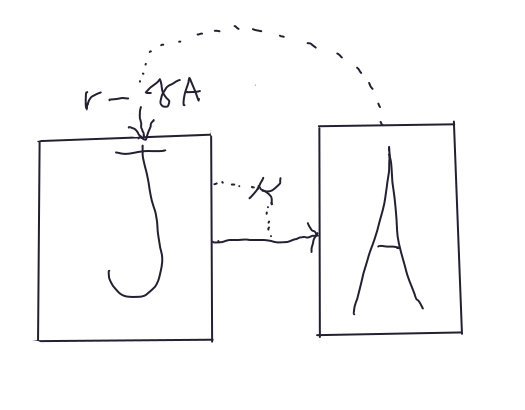
Figura 3.3: Representación gráfica del modelo de crecimiento poblacional con estados de desarrollo.

3.3.1 Relación entre las herramientas matemáticas y los sistemas ecológicos

Los sistemas ecológicos son muy variados, de modo que las herramientas matemáticas disponibles o que conocemos no siempre reflejan ciertos aspectos importantes de los sistemas ecológicos. Un ejemplo notable de ello es la variación de atributos entre individuos de una población. Supongamos que estamos modelando el crecimiento de una población (como en las ecuaciones (3.1) y (3.2)), y la tasa neta de crecimiento depende de la cantidad de adultos reproductores y del crecimiento exponencial de los gametos fértiles en cada adulto reproductor, lo cual ocurre en corales y algunas plantas.

El crecimiento poblacional como tal, puede modelarse con ecuaciones diferenciales ordinarias, mientras que representar el crecimiento de los gametos fértiles dentro de cada adulto en un sistema de ecuaciones ordinarias requiere de otras herramientas mucho más avanzadas.

3.4 Uso de los modelos matemáticos en ecología

Como ya mencionamos anteriormente, una alta proporción de las publicaciones académicas en ecología utiliza modelos matemáticos para predecir. Existen sin embargo otros usos de los modelos matemáticos que se pueden describir en términos generales como analíticos, es decir para analizar y entender cómo los diferentes componentes de un sistema afectan su coportamiento. Otras veces, los modelos se utilizan para medir las respuestas del sistema de interés ante perturbaciones, haciendo muchas simulaciones. Veamos una serie de ejemplos de estos diferentes usos de los modelos.

3.4.1 Analíticos: Dinámicas depredador-presa

En 1928, Vito Volterra (Volterra 1928) desarrolló un modelo matemático para describir cómo varía el número de individuos de una especie de depredador y una presa. Como ya es conocido, este modelo replica muy bien el comportamiento oscilatorio de ambas poblaciones (Figura 3.4).

Figura 3.4: Simulación del modelo Lotka-Volterra.

El comportamiento oscilatorio resulta obvio desde una perspectiva biológica: los depredadores no se pueden reproducir a menos que se alimenten de sus presas, pero cuando hay muchos depredadores, estos consumen las presas disminuyendo sus números, resultando en menor potencial reproductivo para el depredador. Pero matemáticamente, ¿qué hace posible estas oscilaciones? Para responder esta pregunta se necesita entender bajo qué condiciones el sistema de ecuaciones que describe el sistema es estable, es decir cuándo los cambios de ambas poblaciones son cero, es decir bajo qué situaciones el sistema como un todo no experimenta cambio alguno. Este análisis matemático tiene un resultado un tanto sorprendente, pues las condiciones bajo las que dicha condición ocurre son un número imaginario, lo que indica que el sistema como tal es inestable, y por lo tanto siempre tiende a oscilar. El análisis de matemático de los modelos es en su mayoría netamente simbólico y requiere de buenas bases matemáticas.

3.4.2 Simulaciones: Dinámica de enfermedades infecciosas

Los sistemas ecológicos pueden ser muy complejos, lo que resulta en sistemas de ecuaciones igualmente complejos con muchas variables de estado y parámetros, y a la vez hace que el análisis sea muy complicado o imposible. En vista de ello se puede entonces resolver el modelo utilizando herramientas computacionales. Un ejemplo que me gusta mucho es el estudio de la leptospirosis (infección por bacteria del género Leptospira) en ratones Mastomys de Holt, Davis, and Leirs (2006). Los autores formularon un modelo relativamente simple de ecuaciones diferenciales para ver cómo las constantes de su modelo afectan el número de ratones Mastomys y de bacterias Leptospira en el ambiente. Ello lo consiguieron aumentando en 10% los valores de cada una de las constantes y midiendo el cambio tras cada simulación.

Figura 3.5: Las barras (eje \(y\)) indican el cambio proporcional de las diferentes cantidades de interés (color de las barras), ante el aumento del valor de cada parámetro (eje \(x\)), (Holt, Davis, and Leirs 2006).

Los análisis de sensibilidad mostrados en la Figura 3.5 son en realidad una serie de predicciones del sistema. De hecho la predicción generalmente echa mano de modelos matemáticos, así que nos centraremos en resumir: la predicción requiere de la planeación de una serie de escenarios para identificar áreas de intervención (alteración del hábitat por ejemplo) para obtener un resultado favorable de acuerdo con el modelo.

3.4.3 Mal uso de los modelos

Así como existe un uso adecuado de los modelos, es muy fácil darles un mal uso, generalmente relacionado con la calidad de los datos que los respaldan, el grado de entendimiento del sistema en cuestión, y con la relación entre las herramientas matemáticas utilizadas y la naturaleza del problema. Holling (1978) y Karplus (1975), sumarizan los siguientes usos potenciales de los modelos en relación a la calidad de los datos (1-baja calidad, 6-alta calidad):

1. Atención del público
2. Aprendizaje sobre el sistema
3. Prueba de teorías
4. Juegos “qué pasaría si…”
5. Recomendación de acciones
6. Diseño de productos

Haefner (1998) sumariza estos usos potenciales de los modelos de acuerdo con el nivel de entendimiento y calidad de datos en distintas áreas del conocimieto.

Figura 3.6: Relación entre el entendimiento y calidad de los datos, y los potenciales usos de los modelos en las diferentes disciplinas científicas (Haefner 1998).

3.5 Tipos de modelos

La clasificación de los modelos depende de la herramienta que se utiliza para desarrollarlos. En la sección “Cómo construir un modelo”, mencioné brevemente que uno de los pasos es la formulación de un modelo “conceptual”, en forma de un esquema o diagrama. Esta clasificación la podemos ampliar un poco:

1. Modelo conceptual o verbal. Descripciones en lenguaje natural.
2. Diagramático. Representación gráfica (diagramas de flujo o cajas).
3. Físico. Representación a escala de sistema (sistemas hidráulicos).
4. Formal. Matemático (algebráico o sistemas de ecuaciones).

Aquí nos centraremos en ver a mayor profundidad los modelos formales, en clasificar los modelos matemáticos. Haefner (1998) sugiere la siguiente clave dicotómica de clasificación:

1. ¿Las matemáticas representan de manera explícita el proceso de interés?

   1.1. Sí: Modelo mecanístico

   1.2. No: Modelo descriptivo, fenomenológico

2. ¿Las matemáticas representan de manera explícita las condiciones del estado futuro del sistema?

   2.1. Sí: Modelo dinámico

   2.2. No: Modelo estático

3. ¿Las matemáticas representan el tiempo de manera contínua?

   3.1. Sí: Modelo conínuo

   3.2. No: Modelo discreto (el tiempo sólo toma valores enteros, un día, un año)

4. ¿Las matemáticas representan explícitamente el espacio?

   4.1. Sí: Modelo espacialmente heterogéneo

   4.2. No: Modelo espacialmente homogéneo

5. ¿Las matemáticas permiten la ocurrencia de eventos aleatorios?

   5.1. Sí: Modelo estocástico

   5.2. No: Modelo determinístico

3.5.1 Ejemplos

3.5.1.1 Modelo de presa-depredador de Lotka-Volterra (1928)

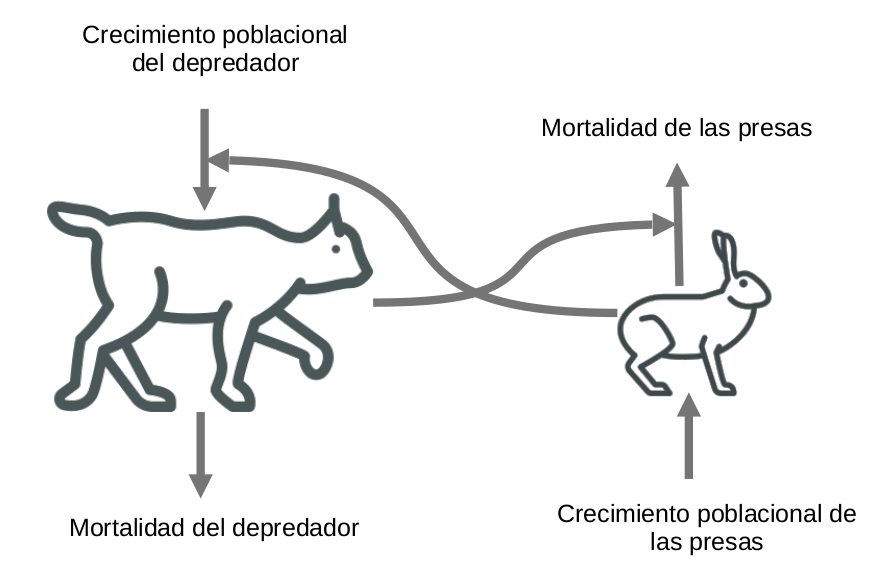
Figura 3.7: Modelo diagramático basado en el modelo matemático depredador-presa de Lotka-Volterra

Este modelo representa cómo cambia el número de liebres y linces a través del tiempo con un sistema de ecuaciones diferenciales. El cambio en los números de individuos depdende de

1. Crecimiento poblacional del depredador en relación a las presas disponibles para que el depredador se alimente
2. Crecimiento poblacional innato de las presas
3. Mortalidad de presas en relación a la cantidad de depredadores
4. Mortalidad innata del depredador

El modelo entonces representa el mecanismo del sistema, por lo que es un modelo mecanístico. Debido a que representa el cambio del número de individuos en el tiempo, es un modelo dinámico. Por el momento no contamos con información suficiente para decir si es contínuo o discreto, pero no hay mención del componente espacial, por lo que podemos suponer que se trata de un modelo espacialmente homogéneo. La solución al modelo clásico de la figura 3.7, muestra un patrón regular, lo cual se debe a que todos los parámetros son constantes, y por lo tanto es un modelo determinista.

3.5.1.2 Modelo del panal de abejas

Wilenski (2003) desarrolló un modelo para representar cómo las abejas construyen un panal, por medio de una serie de reglas que rigen el comportamiento de abejas individuales. Debido a que el mecanismo está representado en el comportamiento colectivo de las abejas, es un modelo mecanístico. El modelo también muestra la progresión de la construcción del panal, por lo que es un modelo dinámico, y debido a que cualquiera de los eventos posibles pueden ocurrir en cualquier momento es en tiempo contínuo. También representa la estructura del panal en unidades espaciales, por lo que es espacialmente heterogéneo. Finalmente, los eventos que ocurren son aleatorios, o sea que el resultado de una realización del modelo será diferente de otra, por lo que es un modelo estocástico. Te invito a explorar este modelo por medio de la aplicación en línea de NetLogo.

A continuación veremos a mayor profundidad los modelos deterministicos y estocásticos.

3.5.2 Modelos determinísticos y estocásticos

Imaginemos que necesitamos un librero, y para ello necesitamos medir las dimensiones del espacio donde lo colocaremos. Solamente contamos con una cinta en pulgadas, pero el carpintero, para hacer el presupuesto, necesita las medidas en centímetros. Entonces para hacer la conversión de pulgadas a centímetros utilizamos el siguiente modelo:

\[\begin{equation} cm = 2.54 \times in \tag{3.3} \end{equation}\]

donde \(in\) son las pulgadas, \(cm\) los centímetros, y \(2.54\) es la constante de conversión. Entonces ya tenemos así un modelo que siempre nos dará la misma respuesta para cada valor de entrada:

• \(2in \rightarrow 2 \times 2.54cm = 5.08cm\)
• \(11in \rightarrow 11 \times 2.54cm = 27.94cm\)

Imaginemos ahora que la constante de conversión no fuera una sola, \(2.54\), sino cientos, o miles de posibles valores cercanos a \(2.54\), y cada vez que resolvemos el modelo (3.3) obtenemos un valor distinto. El primero es un modelo deterministico, siempre da la misma respuesta. El segundo, es un modelo estocástico. Te preguntarás entonces ¿para qué querríamos un modelo que de respuestas inconsistentes? La principal razón es que en ecología, como en otras áreas del conocimiento, los sistemas de estudio son muy variables, y los modelos estocásticos nos sirven para representar esa variabilidad y conocer algunos de los posibles resultados. En pocas palabras, si un sistema es determinista, siempre podemos conocer su comportamiento con alta precisión, mientras que en los estocáticos, no.

3.5.2.1 Deterministicos

En vista de mi comentario “… los sistemas de estudio son muy variables…” tal vez te surja otra pregunta, ¿entonces por qué estudiamos los modelos deterministas? Y no hay una pregunta mmuy sencilla, pero la principal es que son más sencillos. Por otra parte, si pensamos en los modelos desde un punto de vista estadístico, se podría también sugerir que podemos utilizar los modelos determinísticos para estudiar el comportamiento “promedio”, o para caracterizar ese componente, el determinista, de nuestro sistema de estudio. En este sentido, se considera entonces que la mayoría de los sistemas y procesos ecológicos tienen un componente determinístico y uno estocástico. La mejor manera de modelar los sistemas ecológicos, entonces, es utilizando ambos. Por lo tanto, para modelar los sistemas ecológicos con ambos métodos, necesitamos aprender a utilizarlos por separado.

Una de las grandes bondades de los modelos determinísticos es que nos permiten analizar el comportamiento del sistema de estudio. Los modelos de cambio temporal, por ejemplo, han sido muy importantes en el desarrollo de la teoría del caos, la cual sirve para explicar por qué ciertos procesos del mundo natural nunca alcanzan un nivel de estabilidad (¡dinámicas depredaror-presa!).

3.5.2.2 Estocásticos

A diferencia de los modelos deterministas, los estocásticos nunca dan el mismo resultado. Existe un gran variedad de herramientas computacionales y formulaciones matemáticas para conseguir este tipo de comportamiento. En la mayoría de los casos, los modelos deterministas constan de dos componentes, uno determinista, relacionado con los mecanismos propios del sistema de estudio, y uno aleatorio, encargado de generar los eventos posibles o de simular la variación en el componente determinista. Esto lo podemos ilustrar con el modelo de conversión de pulgadas a centímetros:

\[ cm = 2.54 \times in \] el cual es determinista. Sin embargo, podemos formular una versión estocástica, que añada una pequeña cantidad a la conversión determinística cada vez que la calculamos:

\[ cm = 2.54 \times in + \varepsilon \]

donde \(\varepsilon\) es el error que hemos introducido. Técnicamente para hacer esto utilizamos un generador de números aleatorios en el lenguaje de programación R. Veamos una serie de conversiones:

Tabla 3.1: Cinco realizaciones para la conversión de dos pulgadas a centímetros con el modelo determinista y estocástico.

Determinista	Estocástico
5.08	4.570550
5.08	4.689913
5.08	4.847023
5.08	4.922678
5.08	5.115016

Este tipo de inconsistencias de los modelos estocásticos tienen implicaciones muy importantes para el comportamiento de modelos como el de Lotka-Volterra, que veremos más adelante.

References

Haefner, James W. 1998. “Modeling Biological Systems.” Bulletin of Mathematical Biology 60 (3): 597.

Holling, Crawford S. 1978. Adaptive Environmental Assessment and Management. John Wiley & Sons.

Holt, John, Stephen Davis, and Herwig Leirs. 2006. “A Model of Leptospirosis Infection in an African Rodent to Determine Risk to Humans: Seasonal Fluctuations and the Impact of Rodent Control.” Acta Tropica 99 (2-3): 218–25.

Karplus, Walter J. 1975. “The Place of Systems Ecology Models in the Spectrum of Mathematical Models.” IN: New Direction in the Analysis of Ecological Systems, Edited by GS Innis. Simulation Council Proceedings Series 5 (2): 225–28.

Otto, Sarah P, and Troy Day. 2011. A Biologist’s Guide to Mathematical Modeling in Ecology and Evolution. Princeton University Press.

Volterra, Vito. 1928. “Variations and Fluctuations of the Number of Individuals in Animal Species Living Together.” ICES Journal of Marine Science 3 (1): 3–51.

Wilenski, Ulrich. 2003. “NetLogo Honeycomb Model.” http://ccl.northwestern.edu/netlogo/models/Honeycomb.