7 Unidad V - Evaluación de la calidad de datos

7.1 Evaluación de la fiabilidad de datos temáticos

Un mapa temático es una representación geográfica de una variable o un conjunto de variables que tienen características en común. Tal y como se ha visto en estadística las variables pueden ser tanto cuantitativas como cualitativas. Los mapas temáticos pueden estar basados también en diferentes tipos de información geográfica como vectores y rasters. Los mapas tradicionales de uso cotidiano como Open Street Maps no son temáticos, estos reciben el nombre de mapas de referencia (figura 7.1).

Figura 7.1: Ejemplo de mapa de referencia de Open Street Maps

Los mapas temáticos se utilizan para comunicar características específicas del espacio que no son directamente observables, en contraste con los mapas de referencia donde se puede claramente identificar a las estructuras presentes. Por ejemplo, un mapa temático puede representar el estado de bienestar psicológico general de un conjunto de ciudades (figura 7.2).

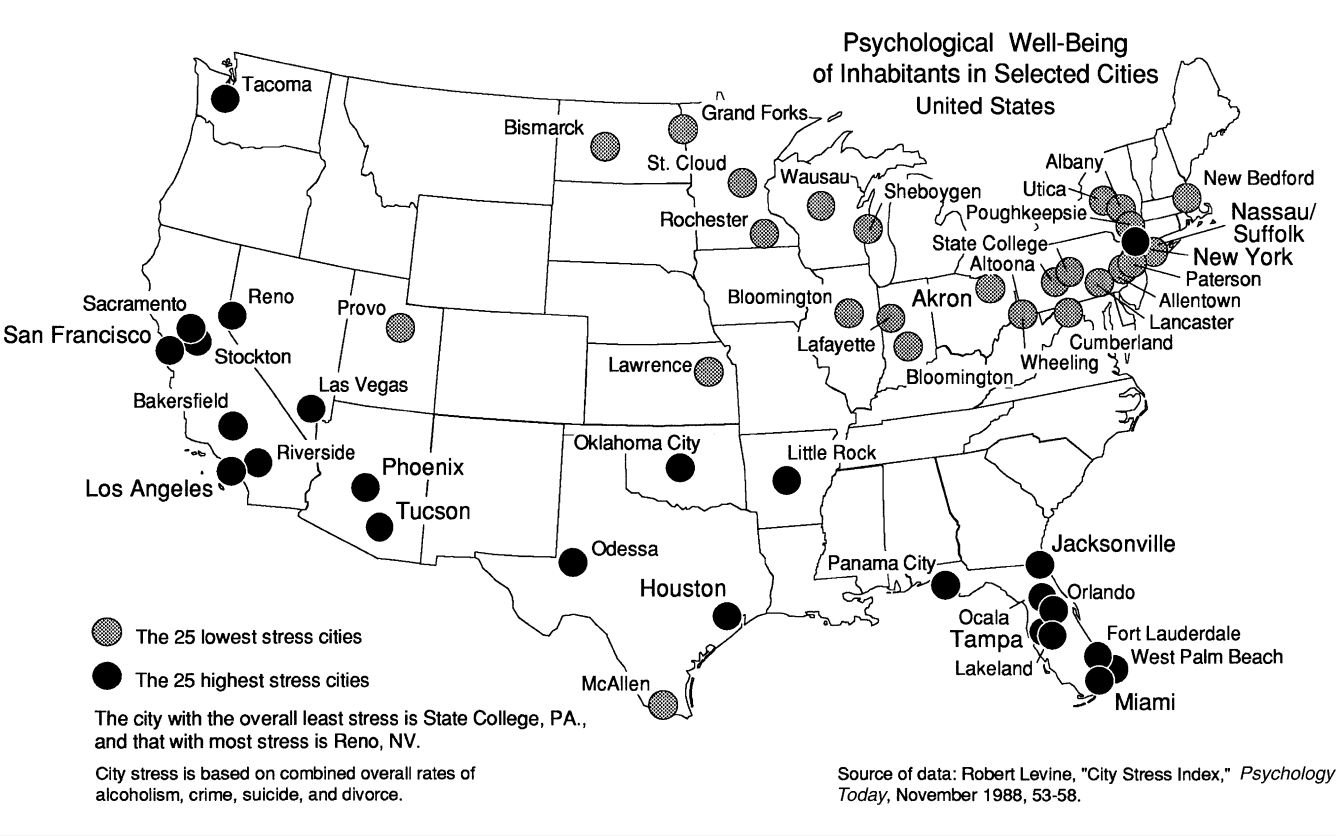
Figura 7.2: Mapa temático del bienestar psicológico en Estados Unidos (Dent et al. 2009).

En los mapas temáticos, los valores, magnitud o cualidades de la variable de interés suele representarse por medio de colores o formas, dependiendo de la naturaleza. Por ejemplo, los valores asociados a puntos pueden representarse tanto con un gradiente de colores como con el tamaño de los puntos (figura 7.3).

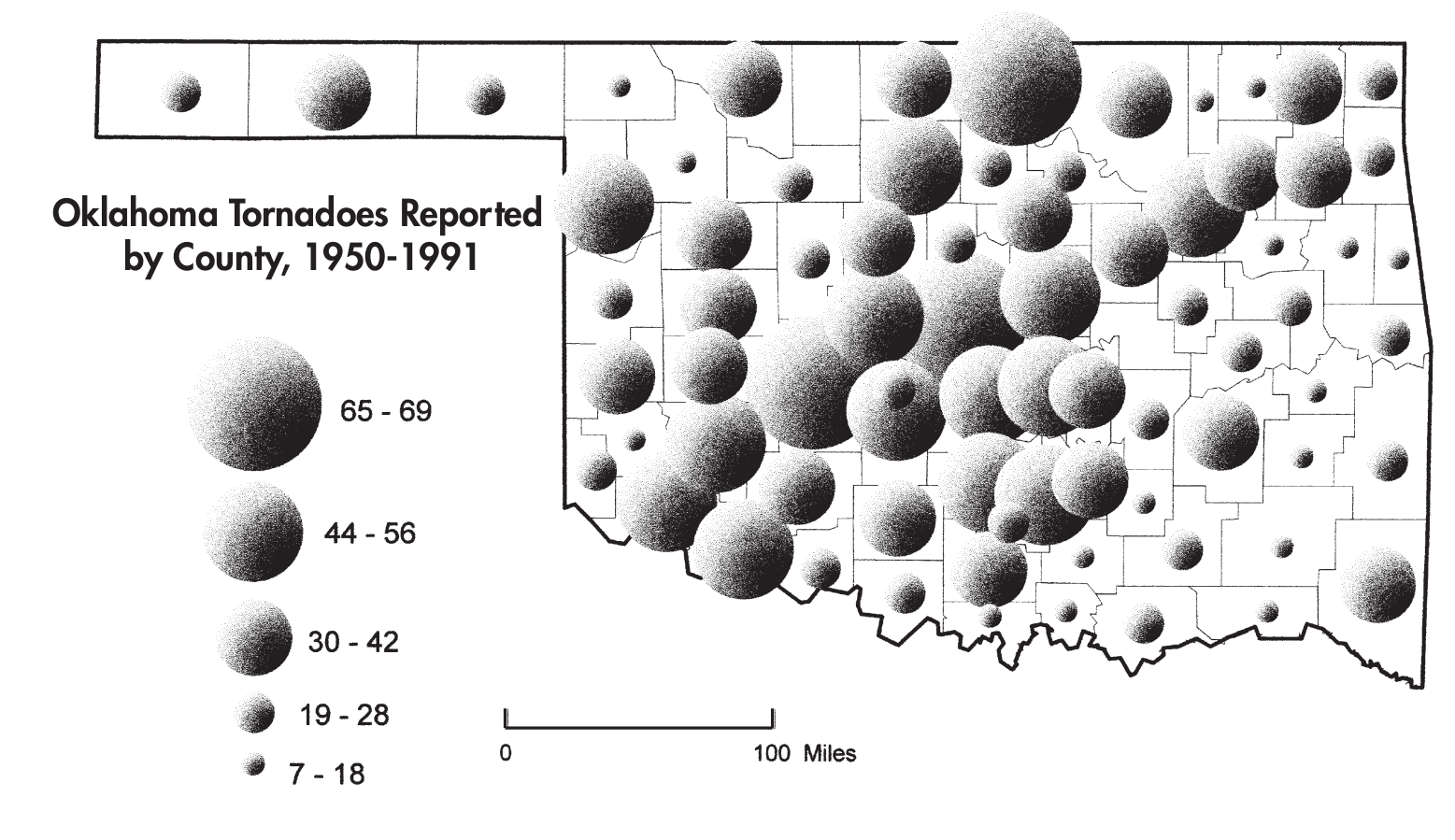
Figura 7.3: Mapa temático del número de tornados reportados por condado en Oklahoma, EU (Dent et al. 2009).

Las variables contínuas también se pueden representar en polígonos vectoriales con paletas de colores. Estos mapas reciben el nombre de coropletas y son muy comunes en algunos campos de conocimiento como la demografía y salud pública, donde las divisiones políticas son de suma importancia.

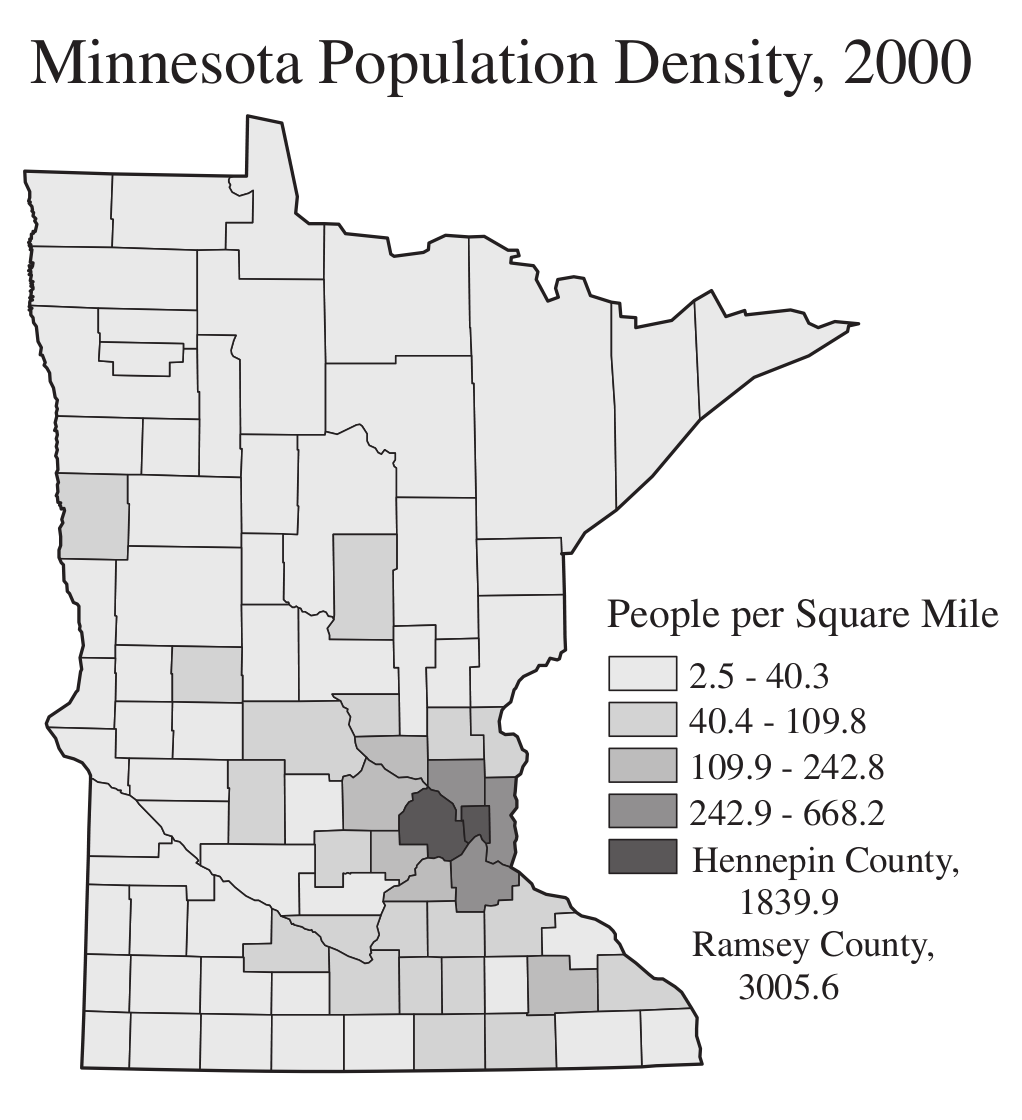
Figura 7.4: Mapa temático del número de habitantes por milla cuadrada (densidad poblaiconal) por condado del estado de Minnesota, EU (Dent et al. 2009)

Los datos temáticos representados en los mapas de las figuras 7.2 - 7.4 son producto de un proceso de observación, y por lo tanto tienen un grado de error y limitaciones importantes. Los errores de las mediciones pueden tener un origen diverso:

• Modo de uso y calibración de instrumentos
• Registro de datos
• Redondeo
• Etiquetado erróneo
• Unidades de medición
• Error humano
• Falta de experiencia
• Método estadístico (interpolación, p. ej.)

Además de todos estos factores hay que tomar en cuenta que las variables que estamos representando en el espacio son en realidad descripciones puntuales (que pueden ocurrir en un espacio pequeño), aplicadas a un área muy grande con una heterogeneidad importante. Es decir, que cada unidad espacial representada en el mapa (los condado en figura 7.4, p. ej.) puede ser dividida en unidades más pequeñas que serán diferentes entre sí. Por lo tanto, es deseable que en la mayoría de los casos se tome en cuenta la incertidumbre de las mediciones.

Hay muchas maneras en que puede medirse la incertidumbre de los datos temáticos:

1. Mediciones previas del grado de error de los instrumentos y/u operadores
2. Incertidumbre medida en el modelo estadístico (en caso de tratarse de un modelo estadístico)
3. Estimación de desempeño predictivo

Las mediciones del grado de error pueden a su vez ser representadas espacialmente para cotejar con el mapeo temático y poder visualizar el grado de error esperado.

7.1.1 Tipos de errores

Las fuentes de error descritas arriba, resultan en errores de distinta naturaleza que se pueden clasificar en errores de (Zhang 2020):

1. Linaje Son los errores relacionados con la reproducibilidad de las estimaciones de los datos temáticos
2. Fiabilidad posicional Son los errores relacionados con los cambios posiionales que degradarán la calidad de las comparaciones subsecuentes
3. Fiabilidad de atributos Se refiere a los errores de clasificación a partir de imágenes de sensores remotos
4. Completitud Se refiere a qué tan completa es la clasificación de los diferentes tipos posibles a partir de imágenes de sensores remotos
5. Fiabilidad temporal Se refiere a que la cobertura temporal de los datos esté reportada adecuadamente

7.1.2 Ejemplo de errores de atibutos y de linaje

En un ejercicio de interpolación, se creó una capa raster de elevación del terreno. Esta capa raster es una aproximación al estado real del terreno, por lo que se puede comparar con un modelo digital de elevación. Es una situación poco usual puesto que en caso de existir on MDE real no habría la necesidad de hacer una interpolación, sin embargo, el ejercicio puede ser muy revelador.

Para hacer la comparación debemos abrir la capa interpolada y el MDE (el estado verdadero del terreno), y sustraer a la capa interpolada la verdader. El resultado será la diferencia entre e estado verdadero y el aproximado en metros. Aquellas regiones con valores negativos corresponderán con regiones donde la aproximación sub-estima la elevación, y los valores positivos son las regiones donde estima mayor altitud de la verdadera:

mde.int <- raster("../Actividades/Analisis-multicriterio/Elevacion.tif")
mde <- raster("../Actividades/Analisis-multicriterio/Elevacion-srtm.tif")

mde <- resample(mde, mde.int)

error <- mde.int - mde

plot(error)

Para tener una idea de la magnitud de las desviaciones en relación a la elevación promedio del terreno, podemos dividir el error entre la desviación estándar. Si recuerdan, \(\mu \pm \sigma\) representa la región donde se encuentra el 69% de los datos, de modo que si dividimos el error entre su desviación estándar podemos ver cuántas desviaciones estándar por arriba o abajo de la media se desvían las aproximaciones:

desvest <- cellStats(error, sd)
plot(error/desvest)

Una medida del error total de la aproximación es el “Root Mean Squared Error” o RMSE, y se calcula como el promedio de la raíz cuadrada del cuadrado del error:

\[ \mathrm{RMSE} = \sum \frac{\sqrt{(X' - X)^2}}{n} \]

donde \(X'\) es la aproximación, \(X\) es el estado verdadero y \(n\) es el número total de aproximaciones o predicciones.

Las unidades de RMSE son las mismas que analizamos, de modo que nos indicará por cuántos metros en promedio falló la aproximación:

rmse <- cellStats(sqrt((mde - mde.int)^2), mean)
rmse

## [1] 37.32274

7.1.3 Errores de fiabilidad posicional y topológicos

La fiabilidad de los datos temáticos no sólo se mide en relación a la incertidumbre en torno al proceso que se representa en el espacio, sino por la precisión con que se representa en el espacio. Por ejemplo, en los mapas de referencia vial, son frecuentes los errores de reprsentación de los caminos, señalamientos viales o edificios. En los datos temáticos este tipo de errores también están presentes, tanto en datos vectoriales como raster. En polígonos, las fronteras de entidades políticas pueden tener errores sustanciales, estructuras lineales pueden tener quiebres o discontinuidades que no están presentes en la realidad 7.5.

Figura 7.5: Ejemplos de errores topológicos y de fiabilidad posicional. Crédito a GIS lounge

7.1.4 Importancia de los errores

Cuando trabajamos con distintas fuentes de error, es inevitable contaminar nuestros análisis con errores de todas las naturalezas posibles. El producto final, entonces debe reconocer las debilidades de cada uno de los insumos para el producto final y cómo éstos afectan su fiabilidad (propagación del error). Muchas bases de datos cumplen con los estándares mínimos para establecer la fidelidad por medio de metadatos, conteniendo información como:

1. Fecha de publicación de la última versión
2. Área de cobertura
3. Escala
4. Sistema de proyección
5. Exactitud y precisión
6. Formato
7. Cobertura temporal (período en que fueron colectados los datos para generarla)

7.2 Evaluación del error de datos continuos

7.3 Propagación del error