3 Unidad I: Introducción al modelado espacial

3.1 Análisis utilizando sistemas de información geográfica

3.1.1 Introducción

En el mundo moderno hay una gran cantidad de procesos y servicios que utilizan información espacial. Más allá de las aplicaciones comerciales que ya todxs conocemos hoy por hoy, los sistemas de información geográficas (SIG) son altamente necesarios para planear muchas de las actividades de las sociedades, por ejemplo para identificar áreas:

donde se permitirá la urbanización
prioritarias de conservación
donde se puede practicar la agricultura
donde se puede producir energías renovables
que se pueden ver afectadas por desastres naturales

Además de identificación de zonas relevantes, también sirven para la cuantificación tanto de superficies como de poblaciones humanas. En ciencas ambientales, nos interesaría aprender a utilizar los SIG para solventar problemáticas ambientales sobretodo aquellas resultado de las actividades del ser humano. Las soluciones ambientales requieren tanto de la identificación espacial como del monitoreo, manejo y mitigación, cuyo éxito puede depender en gran medida de la disponibilidad de información geográfica.

3.1.2 Ejercicio

Visita la página del Socioeconomic Data and Applications Center y navega por los diferentes apartados temáticos que cubren, haciendo una lista con descripciones de mapas que te parezcan interesantes o relevantes.

3.1.3 ¿Qué son los SIG?

Los SIG son programas de computadora especializados en el manejo, análisis y visualización de datos geográficos. Estos últimos a grandes rasgos con una descripción numerica o cualitativa que esté georreferenciada, o bien, que represente la forma o algún atributo de un objeto cuya localización se conoce. Los sistemas de información geográfica por lo general utilizan distintos tipo de datos.

3.1.3.1 Imágenes ráster

Consisten de píxeles que representan valores con alguna paleta de colores

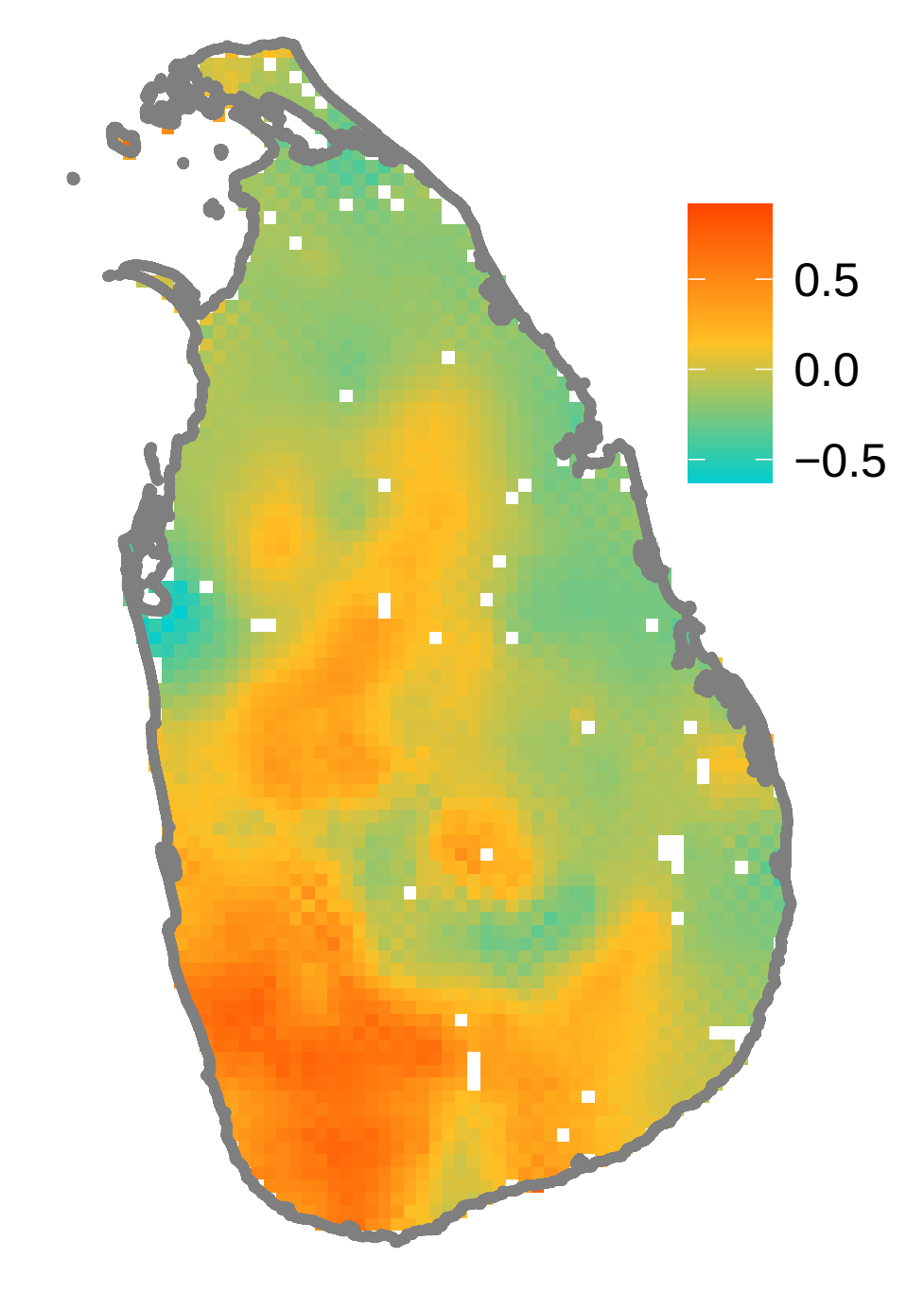
Figura 3.1: Ejemplo de capa ráster de algún atributo ambiental de la isla de Sri Lanka. Cada píxel mide 5 x 5 km.

3.1.3.2 Capas vectoriales

Pueden representar tanto polígonos como líneas. Los polígonos son utilizados para representar entidades políticas como los países o estados. Las capas vectoriales de líneas pueden utilizarse para representar ríos o caminos

## OGR data source with driver: ESRI Shapefile 
## Source: "/home/gerardo/Documentos/Cosas ENES/Materias/LCA/Analisis-Modelado-Espacial/Unidad-I/SL-1/LKA_adm1.shp", layer: "LKA_adm1"
## with 25 features
## It has 14 fields
## Integer64 fields read as strings:  ID_0 ID_1 CCN_1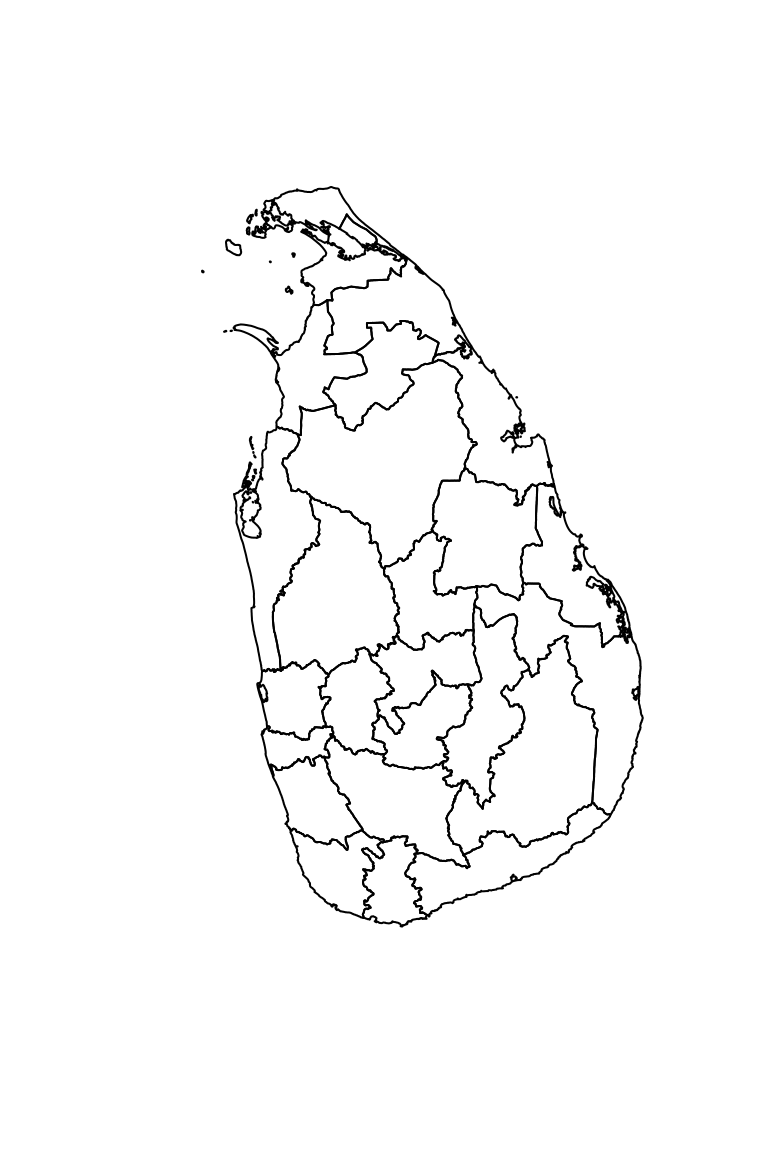

Figura 3.2: Polígono vectorial muestra la isla de Sri Lanka y su división política en distritos.

## OGR data source with driver: ESRI Shapefile 
## Source: "/home/gerardo/Documentos/Cosas ENES/Materias/LCA/Analisis-Modelado-Espacial/Unidad-I/Roads/LKA_roads.shp", layer: "LKA_roads"
## with 500 features
## It has 5 fields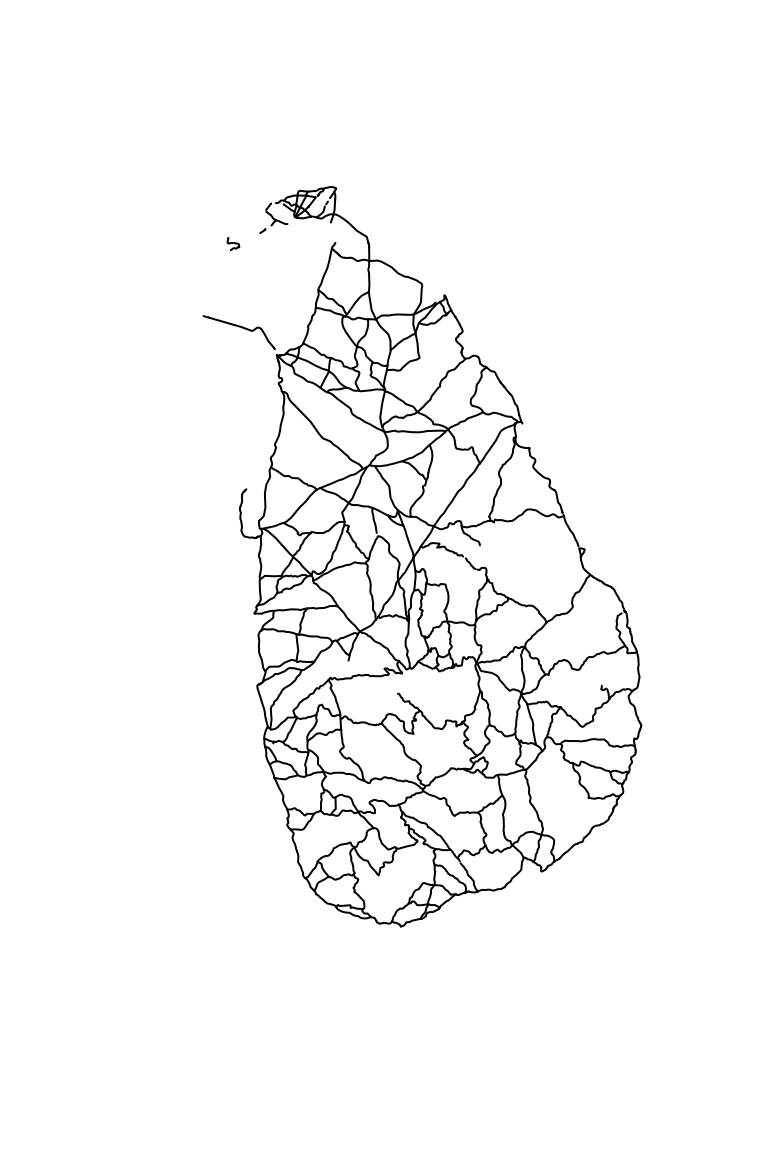

Figura 3.3: Capa lineal muestra la red de carreteras principales de la isla de Sri Lanka.

3.1.3.3 Puntos

Son conjuntos de coordenadas geográficas (\(x, y\)) cartesianas para identificar la localización de un objeto en el espacio.

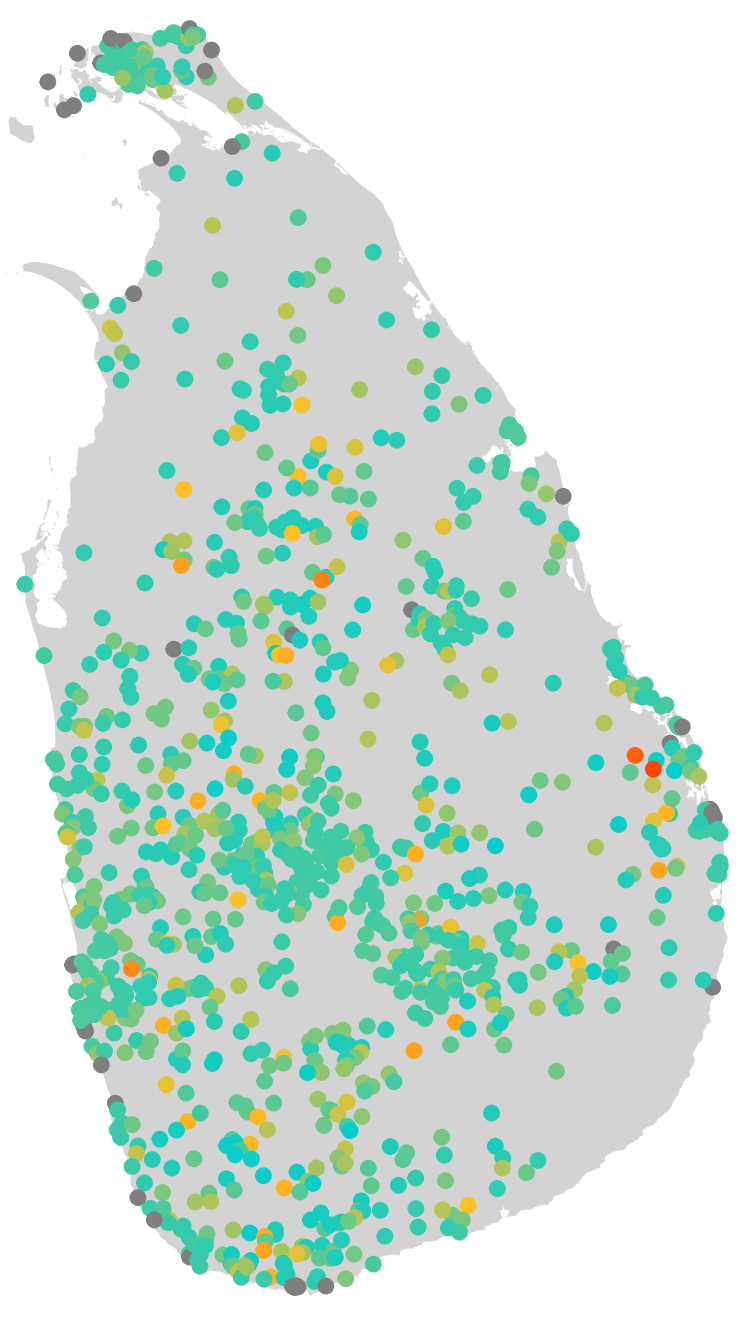
Figura 3.4: Puntos muestran el valor de una medición de alguna variable ambiental en la isla de Sri Lanka.

3.1.3.4 Ejercicio

Vuelve a visitar el Socioeconomic Data and Applications Center y clasifica los mapas que seleccionaste anteriormente de acuerdo con el tipo de datos que consideres que contiene cada uno.

3.1.4 ¿Cómo puedo conseguir un SIG?

Al igual que con los sistemas operativos (Windows, Mac) y las suites de ofimática (Google Docs, MS Office, Libre Office), existen alternativas tanto comerciales (de pago y código cerrado) como libres (tanto de pago –gratis– como de código fuente). Uno de los SIG más completos que existen es ArcGIS, sin embargo costo de la licencia es bastante alto. PAra evitar la necesidad de pagar licencias, en este curso, utilizaremos QGIS (Quantum GIS), Saga y R, pues son gratuitos y cubren todas las necesidades del curso y muchas más. De hecho, estas herramientas son sumamente competentes tanto para estudiantes como para profesionales que requieren de aplicaciones sofisticadas, por lo que la relación costo-beneficio es insuperable.

Para instalar QGIS visita la página web y sigue las instrucciones de instalación para tu sistema operativo. Los demás programas los instalaremos en otra ocasión.

3.2 Modelado espacial

El modelado y análisis espacial puede ser tan variado como los tipos de datos y variables que se pueden representar en el espacio. De manera resumida, el modelado espacial es el desarrollo de representaciones espaciales de añgún fenómeno. Los modelos espaciales pueden ser sencillos, producto de operaciones aritméticas entre distintas variables espacializadas, ó de complejos análisis estadísticos. En este curso veremos aplicaciones de ambas, aunque por su utilidad nos enfocaremos más en los análisis estadísticos.

Los modelos espaciales pueden estar basados en, o utilizar, datos geográficos de cualquier naturaleza: vectores, puntos o ráster. Los productos de estas diferentes naturalezas, utilizados para construir modelos espaciales pueden provenir de muchas fuentes, incluso ser colectados por nosotrxs mismxs. Las fuentes de información para construir los modelos espaciales dependerán de muchos factores como la extensión geográfica. Para regiones pequeñas es perfectamente factible hacerlo nosotrxs mismos, pero para estudios a mayor escala, debemos utilizar repositorios públicos de información que veremos más adelante. A continuación se muestran algunos ejemplos de procesamiento estadístico.

3.2.1 Datos vectoriales

Ejemplos clásicos abundan en la literatura médica, donde típicamente se analiza el número de casos por polígono de alguna enfermedad. Estos análisis consisten, en esencia, de una regresión lineal, donde la variable de respuesta está medida para cada uno de los polígonos de la capa vectorial, y van acompañados de mediciones de alguna(s) variables de respuesta. El ejemplo de abajo, sin embargo es un poco más complicado pues toma en cuenta la similitud entre polígonos vecinos.

La escala de colores indica el número de casos por unidad espacial, y esta representación se llama coropleta.

Casos de cancer labial en Escocia

3.2.2 Ráster

Un tipo de análisis de imágenes ráster muy útil es el desarrollo de mapas de uso de suelo. También existen otras aplicaciones como la estimación de densidad poblacional de humanos a partir de imágenes satelitales.

Estimación de densidad poblacional combinando imágenes satelitales y vectoriales

3.2.3 Puntos

Un ejemplo de este tipo de análisis es el modelado de nichos ecológicos y áreas de distribución, y consiste en utilizar los datos de puntos para generar un ráster que representa la favorabilidad ambiental para un organismo.

Registros de ocurrencia de la serpiente venenosa Bungarus caeruleus y su abundancia potencial estimada en la isla de Sri Lanka

3.2.4 Lecciones

El modelado espacial se distingue de otros tipos de modelación en que, mientras los datos pueden representar mediciones de variables no espaciales (temperatura, tamaño de población, tipo de cobertura vegetal), los datos están descritos por su ubicación espacial y tipo de representación en el espacio. En ocasiones es necesario tomar en cuenta dichas descripciones sobre la situación espacial para hacer el análisis debido a la primera ley de la geografía:

“Los objetos cercanos son más similares entre sí”

A este fenómeno se le conoce como autocorrelación espacial, es decir que una variable con estructura espacial estará correlacionada consigo misma (casi siempre). Por ejemplo en la base de datos de cancer labial, podemos ver que los distritos vecinos tienen niveles de enfermedad más parecidos entre sí.

3.2.4.1 La estructura espacial

Cuando decimos que una base de datos está estructurada quiere decir que cada observación tiene un lugar exacto dentro de la base. El ejemplo más sencillo es de una serie temporal, donde los datos están ordenados en relación al tiempo en que fueron colectados, y sus valores también dependen del tiempo (3.5).

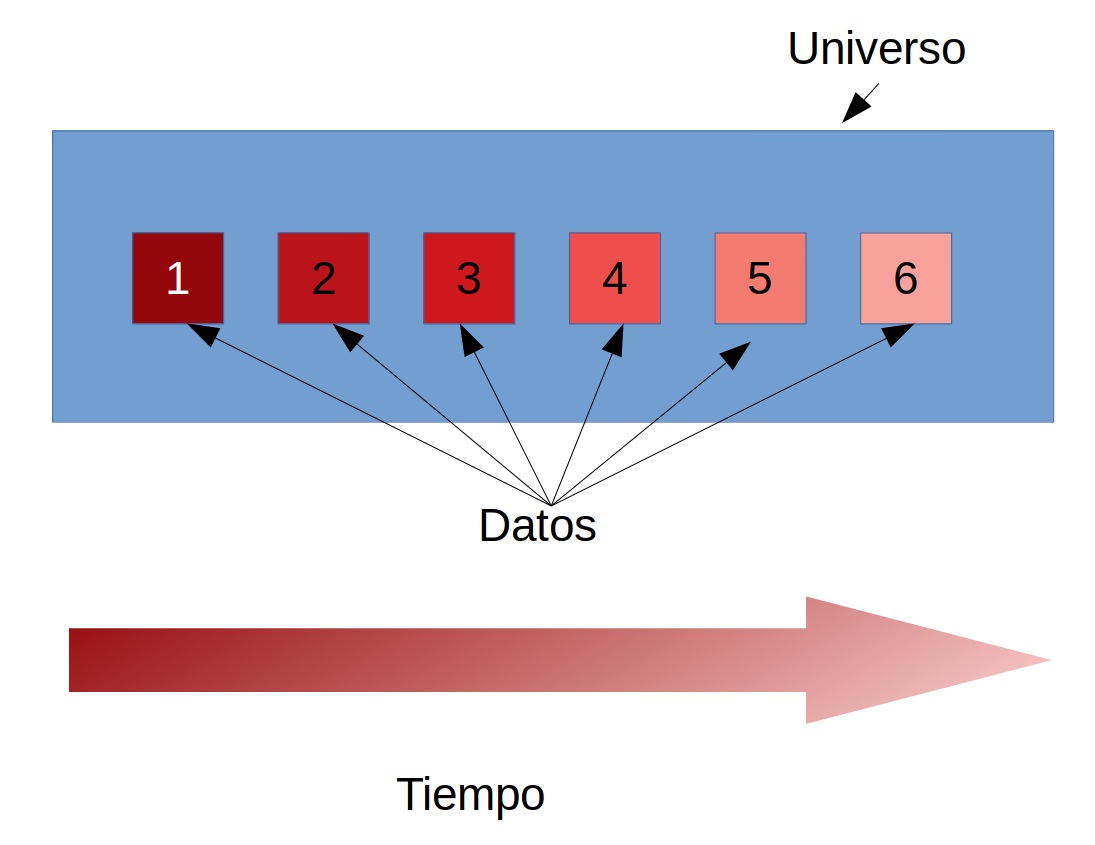
Figura 3.5: Estructura temporal de una base de datos

La repercusión estadística de la estructuración temporal o espacial de los datos es que las observaciones cercanas en el tiempo o espacio no son independientes entre sí. Las observaciones independientes deberían poder tener cualquiera de los valores posibles en la distribución de la variable, pero las observaciones más cercanas tienen valores más parecidos. Por lo tanto es necesario, en muchas ocasiones, utilizar métodos estadísticos que permitan separar esos efectos de la proximidad espacial o temporal de los efectos de otras variables (temperatura, vegetación, etc.). A este fenómeno se le conoce como Autocorrelación espacial o temporal, es decir, que una variable está correlacionada consigo misma.

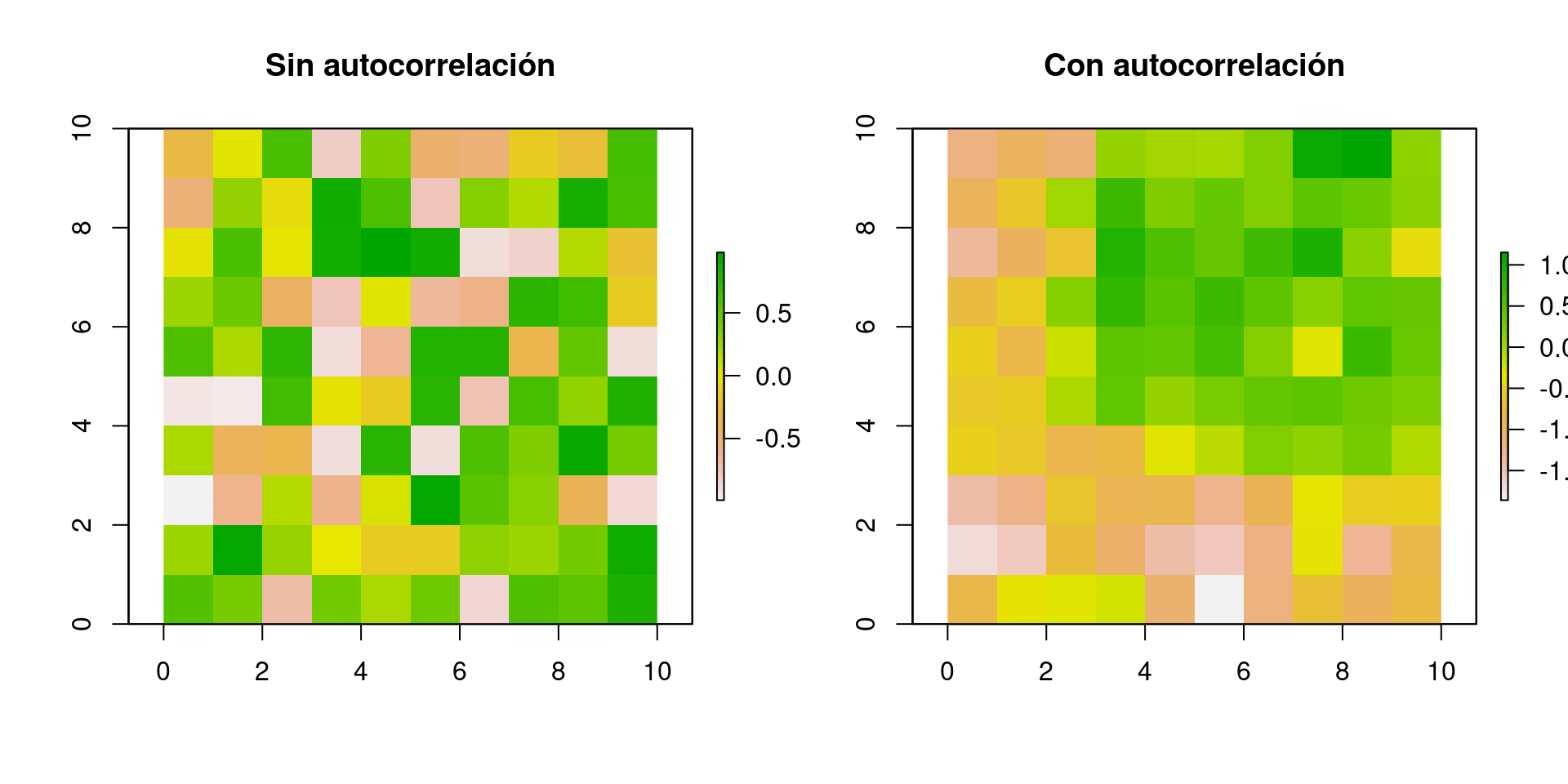
Figura 3.6: Ejemplos de capas ráster con y sin autocorrelación.

Los métodos que combinan la modelación estadística y aquellos utilizados para medir y estimar la autocorrelación, son lo que distingue a la modelación estadística de la modelación espacial.

Análisis y Modelado Espacial