6 Unidad IV - Análisis multicriterio

El análisis multicriterio es una técnica para la síntesis del conocimiento e integración de diferentes tipos de información para ayudar a la toma de decisiones. En SIG y ciencias ambientales se usa principalmente para la gestión territorial. El nombre multicriterio, se debe a que se basa en la modificación de un conjunto de variables (en SIG generalmente son raster), cada una con criterio específico, por ejemplo aplicar un umbral < 1000 msnm a un modelo digital de elevación. Cuando se diseña una diversidad de criterios a aplicar al conjunto de variables que se combinarán para identificar las zonas que cumplen con los diferentes criterios, el producto se puede usar para tomar decisiones informadas.

6.1 Dimensiones espaciales del análisis multicriterio

El uso de análisis de multicriterio con sistemas de información geográfica se basa en operaciones aplicadas a datos espaciales (generalmente raster), para aplicar los criterios y combinarlos. Los criterios se refieren a valores umbral que se aplicarán, por ejemplo:

1. \(\mathrm{Temp} > 5 \mathrm{°C}\)
2. \(\mathrm{Elev} \geq 500 \mathrm{\ msnm}\)
3. \(0 > \mathrm{Población} \mathrm{\ km^{-2}} \leq 1000\)
4. \(\mathrm{Precipitación\ anual} \approx 1000 \mathrm{\ mm}\)

Cada uno de los criterios que se tomen en cuenta siempre deben de responder a algún aspecto relevante del proceso sobre el cual se deben de tomar decisiones sobre gestión territorial.

Posteriormente al diseño de criterios a aplicar a cada variable, se diseña el modelo para combinarlos. El resultado de aplicar los criterios son variables raster binarias (valores de 0 y 1), donde 0 representa ausencia del criterio, y 1 su presencia (Figura 6.1).

library(raster)
r <- raster("../Unidad-II/Capas-ejemplo/bio1.tif")
r1 <- r > 150 #aplicación del criterio
par(mfrow = c(1, 2))
plot(r); plot(r1)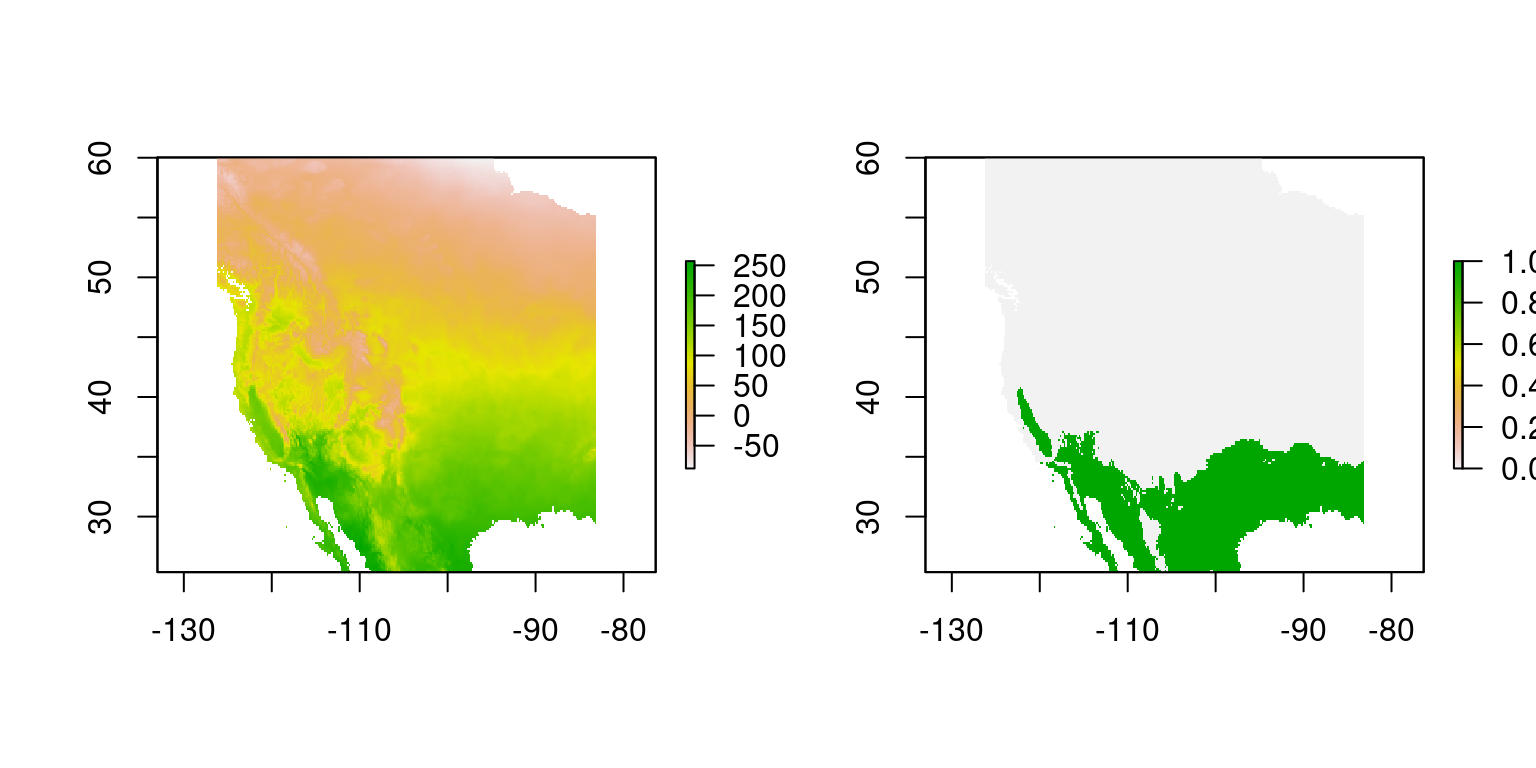

Figura 6.1: Ejemplo de criterio de temperatura > 15 °C (derecha) a una capa de temperatura anual promedio para norte américa (izquierda). En verde se muestran todas las zons que cumplen con el criterio aplicado, y en gris las zonas que no lo cumplen.

Debido a que los raster son en su mayoría, representaciones geográficas de variables cuantitativas, existe un gran número de operaciones que podemos realizar con ellos. Por ejemplo, si multiplicamos los raster de la figura 6.1, obtenemos:

r2 <- r * r1
plot(r2)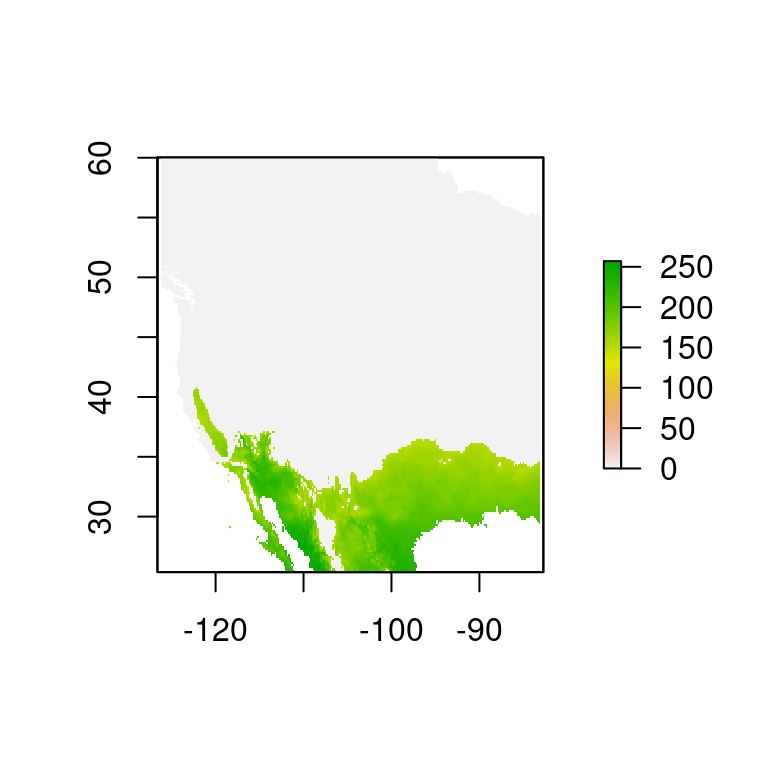

Figura 6.2: Producto de rasters muestra la temperatura de las regiones únicamente con temperatura promedio mayor a 15 °C.

Ahora, para ver la suma de criterios, necesitaríamos importar otra variable, pues no tendría sentido añadirle \(1 \mathrm{°C}\) a la temperatura anual promedio. Acá, importamos el rango anual de temperatura (máxima promedio - mínima promedio), y aplicamos el criterio de \(\geq 15\mathrm{°C}\), para encontrar las zonas donde la diferencia entre las temperaturas máximas y mínimas promedio es mayor ó igual a 15°C.

r.1 <- raster("../Unidad-II/Capas-ejemplo/bio2.tif")
r.12 <- r.1 >= 150
par(mfrow = c(1, 2))
plot(r.1); plot(r.12)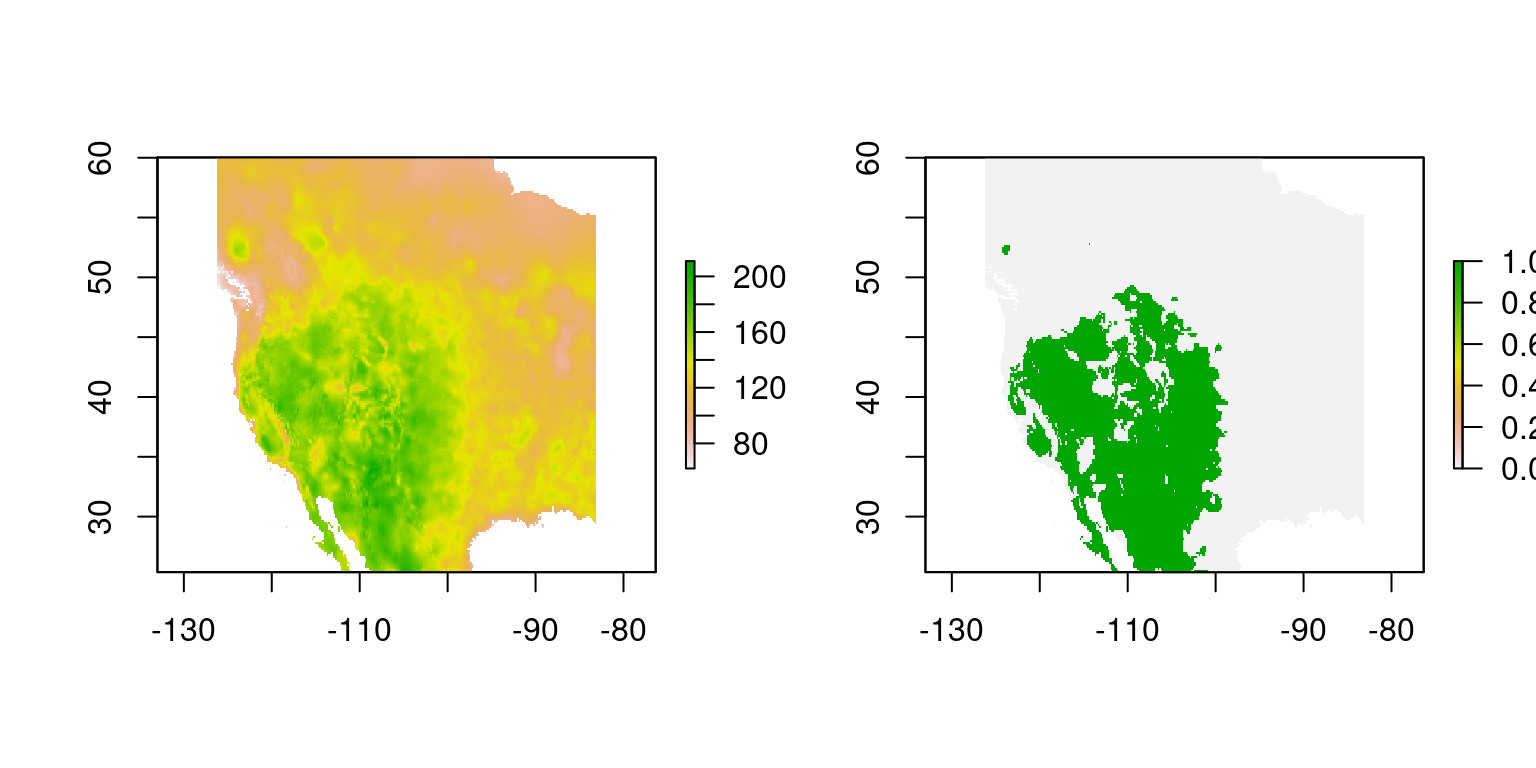

Figura 6.3: Criterio de rango de temperatura mayor o igual a 15°C.

Entonces, ahora sí, podemos identificar las zonas que cumplen con uno o dos de los criterios, temperatura anual promedio mayor a 15°C y rango de temperatura mayor o igual a 15°C:

suma.crit <- r1 + r.12
plot(suma.crit)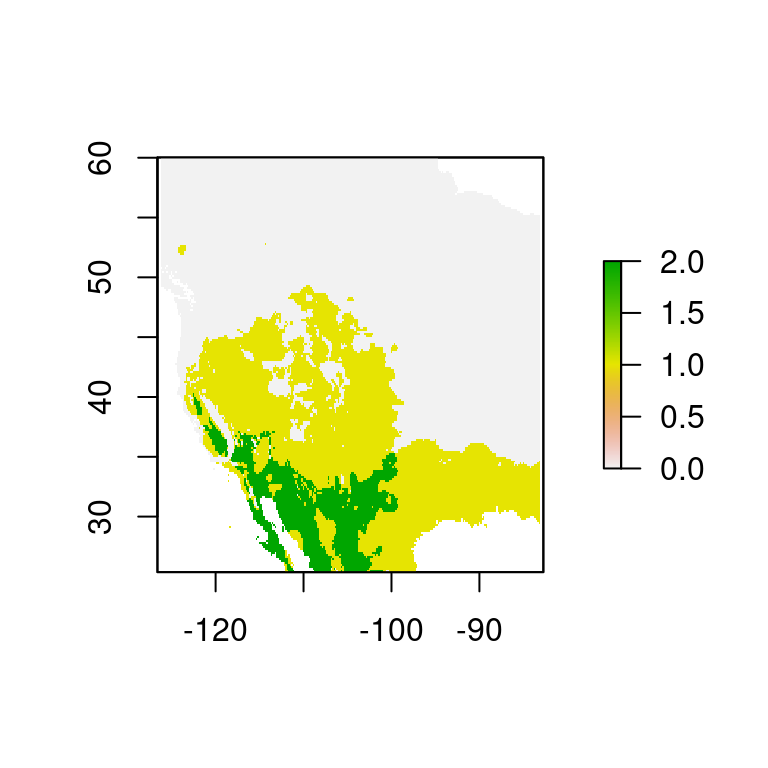

Figura 6.4: Las zonas grises indican que no se cumple ninguno de los criterios, las amarillas son aquellas donde spolo se cumple uno de los criterios y en las verdes se cumplen ambos.

En lugar, si hacemos multiplicación de criterios, obtenemos

prod.crit <- r1 * r.12
plot(prod.crit)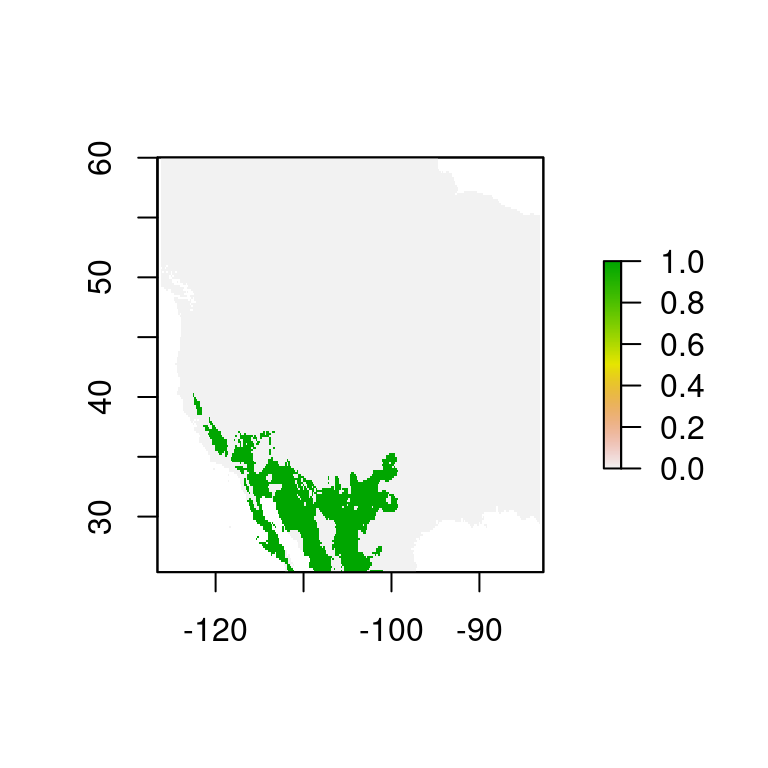

Figura 6.5: Multiplicación de criterios resulta únicamente en las áreas que cumplen con ambos criterios

las áreas que cumplen tanto con el criterio 1 como con el criterio 2. La sustracción por el contrario:

resta.crit <- r1 - r.12
plot(resta.crit)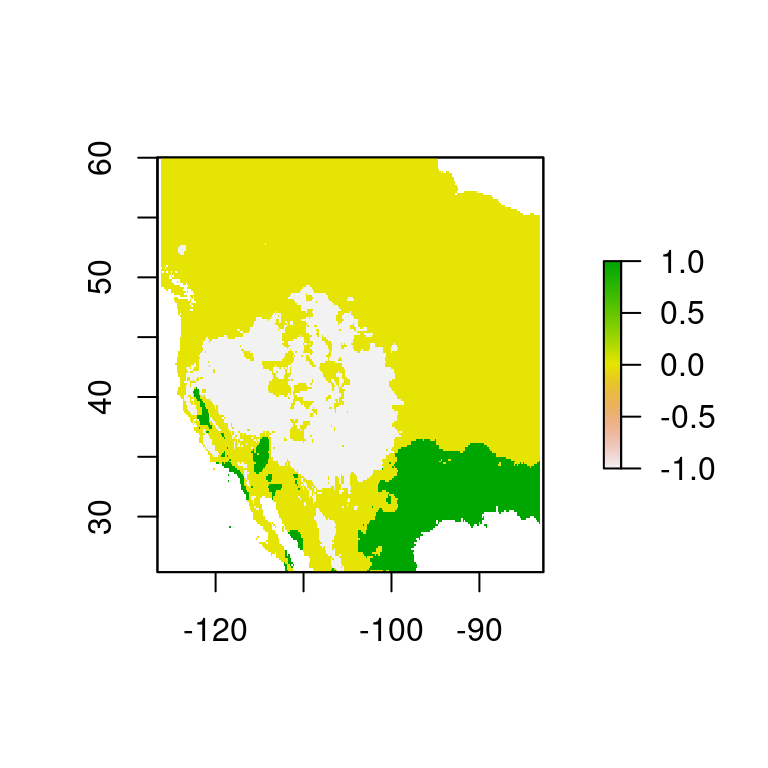

Figura 6.6: Sustracción de criterio 1 menos criterio 2

representa:

1. Verde: Zonas donde la temperatura anual promedio es \(> 15 \mathrm{°C}\).
2. Gris: Zonas donde la temperatura anual promedio es \(> 15\mathrm{°C}\) y el rango de temperatura es \(\leq 15\mathrm{°C}\)
3. Amarillo: Zonas donde la temperatura anual promedio es \(> 15\mathrm{°C}\) y el rango de temperatura es \(\geq 15\mathrm{°C}\) y zonas donde la temperatura anual promedio es \(< 15\mathrm{°C}\) y el rango de temperatura es \(\leq 15\mathrm{°C}\)

### Conclusión

Es de suma importancia identificar las operaciones aritméticas que se harán entre criterios para que el resultado final sea consistente con los objetivos planteados del análisis multicriterio. Por lo tanto, los objetivos deben ser planteados a priori y deben permitir identificar las variables espaciales que se necesitan para llevarlo a cabo. Aquí se mostró un análisis multicriterio sumamente sencillo utilizando únicamente datos raster. En la práctica quizás nos veamos en la necesidad de combinar puntos, líneas vectoriales, polígonos y raster. Por lo tanto hay que aprender también cómo se puede combinar los diferentes tipos de datos espaciales.