7 Unidad V: El desarrollo de un modelo de nicho o de distribución

7.1 Selección de proyección geográfica

La tierra es un elipsoide, y uno de los retos geométricos más grandes es la representación de su superficie como un plano. Para entender la complejidad del problema, pensemos en la tierra como una pelota de playa que cortamos y tratamos de extender sobre una mesa. En este proceso nos damos cuenta de que obtenemos algunas porciones del material bien extendidas y otras con arrugas. Esto mismo sucede cuando intentamos representar la tierra como una superficie plana. Para solucionar este problema se han propuesto varias soluciones, proyectando la superficie terrestre en diferentes formas geométricas como:

1. Plano tangente a algún punto específico
2. Cono que toca la superficie terrestre en algún paralelo
3. Cilindro que toca la superficie en el ecuador

Todas estas metodologías resultan en distorsiones diferentes, como de áreas o ángulos. Es imposible representar correctamente todos estos aspectos, de modo que es importante seleccionar adecuadamente la proyección para hacer nuestros análisis. En el análisis de procesos de puntos el interés es la densidad por unidad de área, de modo que siempre tenemos que buscar una proyección que conserve las áreas a expensas de la representación adecuada de los ángulos.

Las proyecciones que conservan las áreas llevan nombres como Equal area, y las hay desarrolladas para regiones específicas. Puedes visitar esta página para ver cómo las diferentes proyecciones afectan la representación de la superficie terrestre.

Para ayudarnos a seleccionar el sistema de proyección adecuado para nuestros análisis, necesitamos identificar el nombre de la proyección que necesitamos. La gran mayoría de los datos geográficos disponibles están en proyección WGS84, que es una proyección cilíndrica. Existe una base de datos de proyecciones geográficas con códigos de identificación que se llaman EPSG. En esta biblioteca de proyecciones el código EPSG para la proyección WGS84 es EPSG 4326. Todas las proyecciones tienen un identificador EPSG, y están desarrolladas para representar lo mejor posible las áreas ó formas de regiones geográficas específicas. Para regiones cerca del ecuador, las proyecciones cilíndricas son las más adecuadas, a latitudes medias las cónicas y para los polos las proyecciones planares (tangentes a las superficie).

Las proyecciones diseñadas para México están agrupadas con el nombre ITRF2008. Para buscar los identificadores EPSG puedes dirigirte a https://epsg.io/ y hacer la búsqueda específica para el país donde harás el análisis. Una vez obtenidos los resultados, las proyecciones geográficas con áreas iguales se pueden filtrar en el menú a mano derecha bajo la liga “projected”.

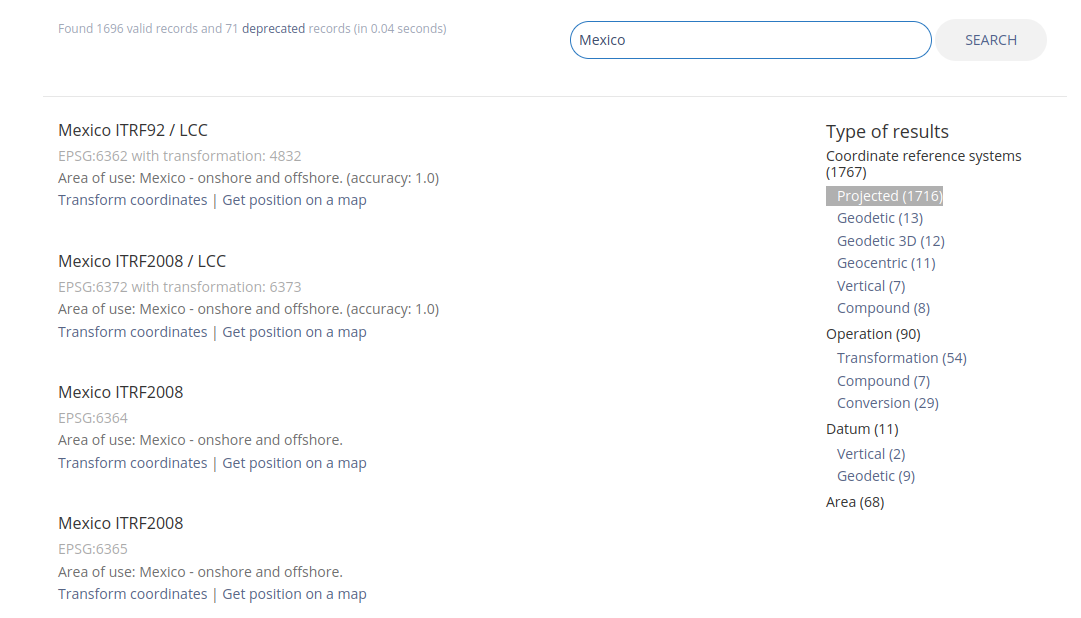
Figura 7.1: Página de la biblioteca de EPSG, con la búsqueda para México.

Una vez filtrada la búsqueda para sistemas de coordenadas proyectadas, podemos dar click en las ligas “Get position on a map” para identificar la región geográfica para la cual fue diseñado ese sistema. En el ejemplo seleccioné el último elemento de la lista, que optimiza la representación de la península de Yucatán.

Figura 7.2: Liga para ver la región geográfica

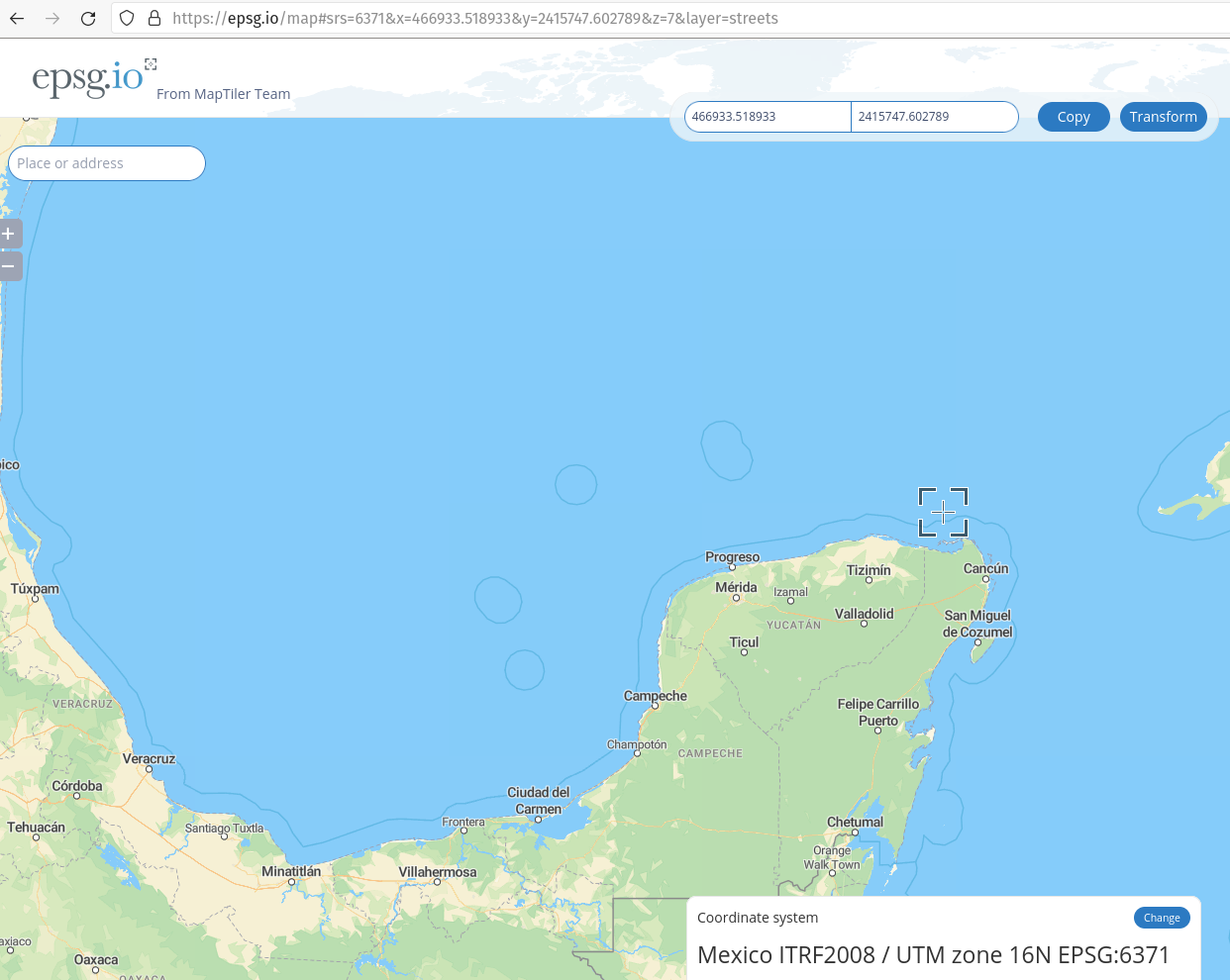
Figura 7.3: Región geográfica para la proyección ITRF2008 centrada en la península de Yucatán, con identificador EPSG número 6371.

7.1.1 Transformando los sistemas de coordenadas en R

Para hacer transformaciones de coordenadas en R es necesario, primero que nada, indicarle a R cuál es el sistema de coordenadas de los datos a convertir. Este paso se hace al inicio del script donde comenzamos los análisis de modo que todos los pasos posteriores se hagan con los datos en la proyección correcta.

Como ejemplo veamos la transformación de las capas raster que hemos estado utilizando en todos los ejemplos. Comenzaremos por preguntarle a R cuál es la proyección actual:

proj4string(s)

## [1] "+proj=longlat +datum=WGS84 +no_defs"

En este caso, no tenemos que indicar la proyección, por lo que podemos hacer la transformación:

s.it08 <- projectRaster(s, crs = CRS("+init=epsg:6371"))
plot(s.it08)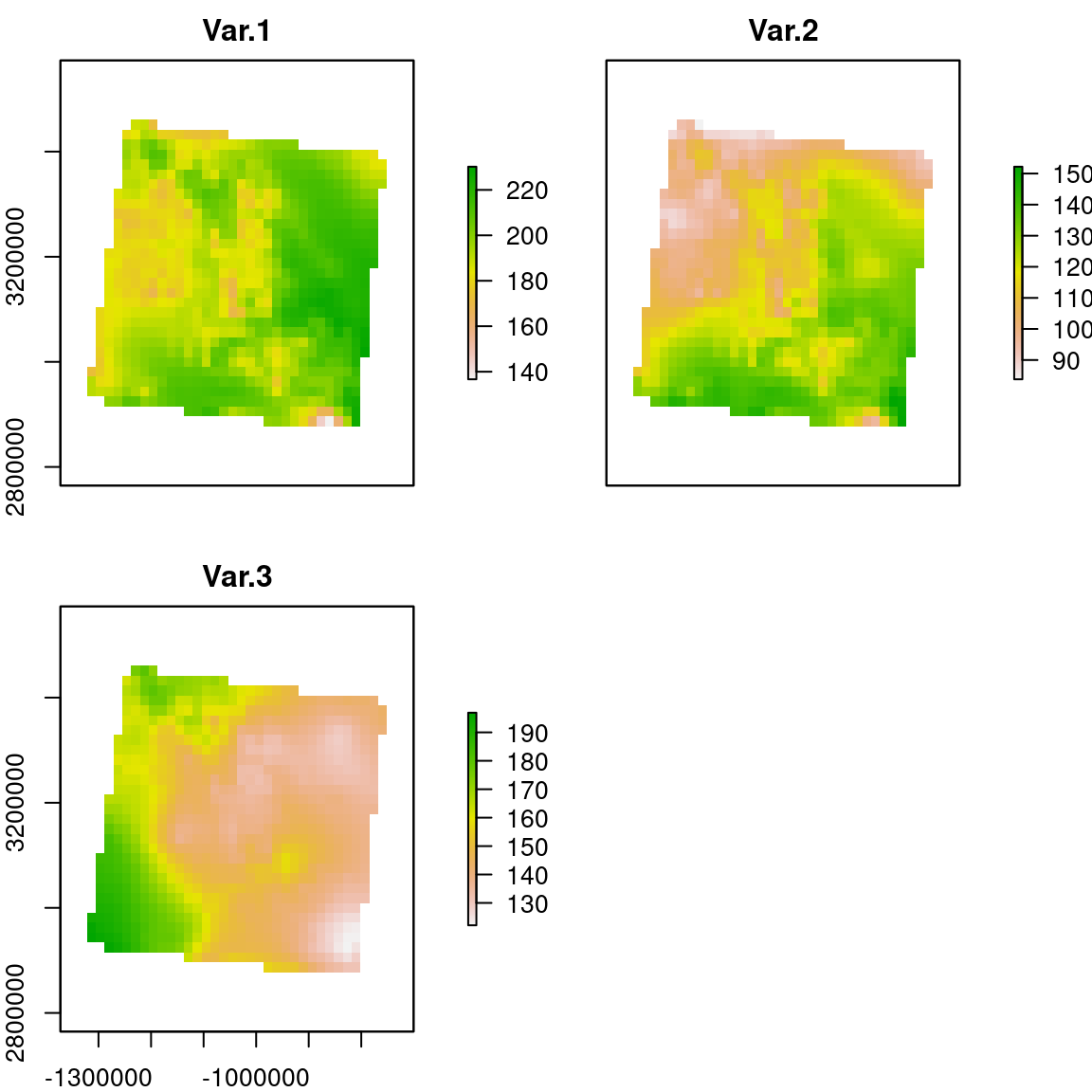

Para transformar los puntos necesitamos una función distinta, y en este caso, sí declarar la proyección inicial de los puntos, después de transformarlos en un objeto espacial:

puntos <- read.csv("../Datos-ejemplos/Puntos-tutorial-2.csv")
coordinates(puntos) <- ~x+y

Declaración de la proyección, la cual es WGS (EPSG4326):

proj4string(puntos) <- CRS("+init=epsg:4326")

Transformación al nuevo sistema de coordenadas:

puntos.it08 <- spTransform(puntos, CRSobj = CRS("+init=epsg:6371"))

Ahora comprobamos que los puntos estén dentro de la ventana de trabajo:

plot(s.it08[[1]]); points(puntos.it08)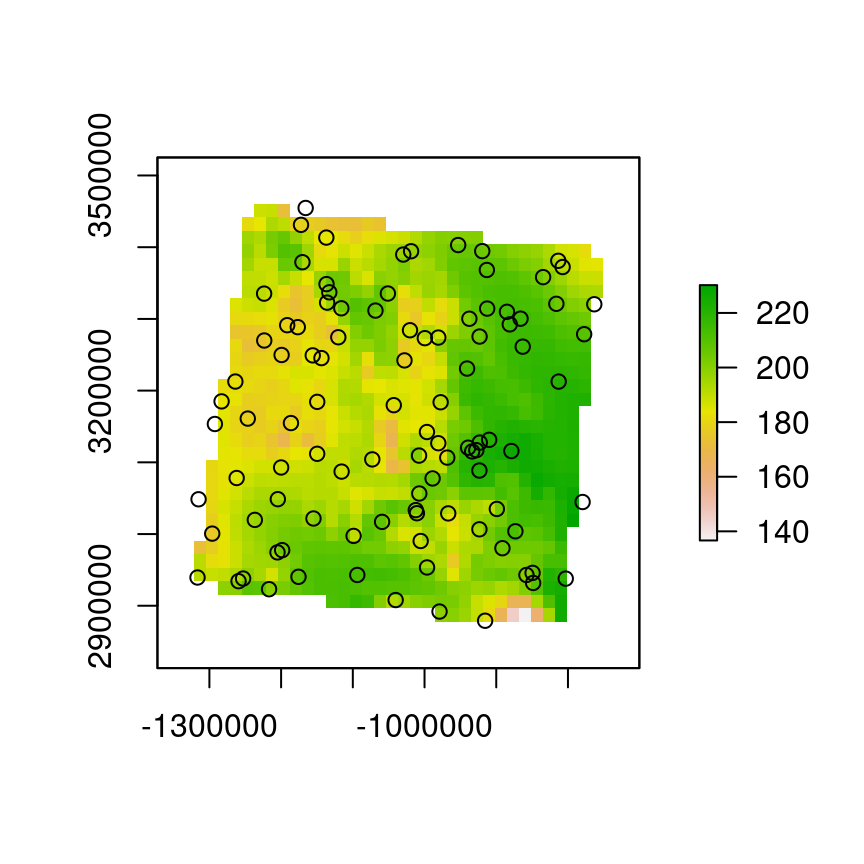

7.2 Selección de variables ambientales

Para ajustar un modelo de puntos necesitamos identificar las variables ambientales que incluiremos con sus fórmulas respectivas. Hasta este momento nos hemos enfocado en ajustar modelos muy sencillos con pocas variables, por lo que aún nos queda por identificar una serie de variables adicionales que podrían explicar la correlación espacial de nuestros datos. El procedimiento para identificar más variables ambientales es el mismo que anteriormente, pero necesitamos comenzar con un objeto del tipo stack que contenga más variables.

En 2005 Robert Hijmans publicó la famosa base de datos WorldClim, donde desarrolló un conjunto de 19 variables compuestas que denominó variables bioclimáticas, que representar diferentes combinaciones de temperatura y precipitación, una en relación a la otra. La lista completa de variables bioclimáticas es:

1. bio1 = Temperatura anual promedio
2. bio2 = Rango diurno de temperatura (promedio de temperatura máxima - mínima)
3. bio3 = Isotermalidad (bio2/bio7) (* 100)
4. bio4 = Estacionalidad de la temperatura (Desviación estándad \(\times 100\))
5. bio5 = Temperatura máxima del mes más cálido
6. bio6 = Temperatura mínuma del mes más frío
7. bio7 = Rango anual de temperatura (bio5-bio6)
8. bio8 = Temperatura promedio del cuarto más húmedo
9. bio9 = Temperatura promedio del cuarto más seco 10 bio10 = Temperatura promedio de cuarto más húmedo
10. bio11 = Temperatura promedio del cuarto más frío
11. bio12 = Precipitación anual total
12. bio13 = Precipitación del mes más húmedo 14 bio14 = Precipitación dle mes más seco
13. bio15 = Estacionalidad de la precipitación (coeficiente de variación)
14. bio16 = Precipitación del cuarto más húmedo
15. bio17 = Precipitación del cuarto más seco 18 bio18 = Precipitación del cuarto más cálido

Como resulta evidente agunas de estas variables bioclimáticas son construidas con base en otras variables bioclimáticas (bio3 y bio7, p. ej.). Por ello, algunas de estas están correlacionadas y no deben ser incluidas en el mismo modelo:

• bio3 es incompatible con bio2 y bio7 simultáneamente
• bio7 es incompatible con bio 5 y bio6 simultáneamente

Entonces el proceso de identificación de variables tiene que tomar en cuenta esta colinealidad de facto y toda aquella que pueda ser identificada estadísticamente.

Además de estos estas cualidades de las que debemos estar conscientes, también es necesario tomar en cuenta que algunas de las variables bioclimáticas suelen tener artefactos espaciales, es decir características geográficas que no representan atributos reales de la variación espacial del clima. Estos artefactos se presentan más comunmente en las variables bio8, bio9 y bio14. Entonces, antes de comenzar con la selección de variables bioclimáticas, es buena práctica revisar si estas variables presentan los artefactos mencionados para el área de estudio (ejemplo).

Para hacer la lista de variables compatibles, podemos utilizar las gráficas de correlación por pares, como se ha mostrado anteriormente. A partir de estas gráficas comenzamos a hacer la lista de variables compatibles entre sí con base en un coeficiente de correlación tolerado. Como regla de dedo utilizamos el valor \(-0.7 \geq r \leq 0.7\).

Las listas de covariables compatibles pueden ser formuladas con el reemplazo de variables no compatibles entre sí. Por ejemplo, si bio1 y bio5 están correlacionadas entre sí, pero ninguna de las dos está correlacionada con bio2, y bio3, las listas de variables compatibles sería:

1. bio1, bio2 y bio3
2. bio2, bio3 y bio5
3. bio1, bio2
4. bio1, bio3
5. bio2 y bio3
6. Todas las combinaciones que surjan

Con base en estas listas y las gráficas de intensidad de puntos en relación a las diferentes variables podemos proponer las fórmulas para los modelos basadas en los tipos de respuestas que identifiquemos.

7.3 Validación del modelo

La validación es un paso esencial en el proceso del desarrollo de un modelo, pues informa al usuario de la capacidad predictiva y la magnitud de los errores esperados. En modelación correlativa de nichos ecológicos hay prácticas estándar que consisten de:

1. Proponer modelo
2. Dividir presencias es datos de ajuste y de validación
3. Medir capacidad predictiva de un modelo utilizando los datos de validación
4. Seleccionar modelo que mejor prediga los datos de validación

La metodología general de modelación de nichos fue desarrollada así porque las herramientas espacialmente explícitas y estadísticamente robustas como los procesos de puntos no se habían adoptado en ecología hasta hace unos 10 años que se demostró que son equivalentes a metodologías de aprendizaje de máquinas desarrolladas específicamente para modelar distribuciones de organismos como MaxEnt (Renner and Warton 2013). Con procesos de puntos, es posible proponer y seleccionar modelos con base en la larga tradición de modelación estadística frecuentista que ya es muy bien entendida y para la cual se han desarrollado criterios claros para medir qué tan bien un modelo representa los datos (como el de información de Akaike). Sin embargo, también se ha demostrado, que estos criterios pueden fallar cuando los datos analizados involucran correlación espacial (Velasco and González-Salazar 2019). Por lo tanto, es recomendable continuar aplicando algunos de los métodos de validación que se comenzaron a adaptar a la modelación de nichos ecológicos desde sus etapas tempranas.

7.3.1 Pruebas de validación estadística

7.3.1.1 Área bajo la curva

Estas tienen como objetivo dotar al usuario de los modelos de la información necesaria para establecer un balance entre distintos errores de predicción. Hasta hace unos años, la métrica de elección era el área bajo la curva del operador característico (AUC-ROC por sus siglas en inglés). Este método pretende evaluar la capacidad de un modelo de distribución de distinguir entre presencias de ausencias. Un modelo perfecto es aquel que clasifica correctamente todas las presencias como presencias y las ausencias como ausencias, lo que resulta en un AUC = 1. Cuando el modelo no distingue presencias de ausencias mejor que un predictor aleatorio AUC = 0.5. En un escenario ideal, lo datos de presencia y ausencia que se utilizan para calcular el AUC son datos que no te utilizaron para ajustar el modelo, por lo que la partición de la base de datos es necesaria. Esta prueba de desempeño predictivo, naturalmente sólo es útil cuando se cuenta con datos de ausencia verdadera y el método de modelación es adecuado para ese tipo de datos, y por lo tanto no es adecuada para medis el desemeño de modelos bsados en procesos de puntos.

Además de ser una prueba inadecuada para datos de sólo presencia, el AUC, tiene graves deficiencias para modelación de áreas de distribución. La mayor de ellas tiene que ver con el criterio espacial para asignar los puntos de ausencia, si éstos se encuentran en regiones muy lejanas a los puntos de presencia, el modelo podrá discriminarlas muy fácilmente, generando la falsa sensación de que es muy bueno para predecir (Barve et al. 2011) (figura ??). En este respecto, se recomienda entonces que las ausencias utilizadas provengan de regiones que sean accesibles para la especie pero no esté presente por las condiciones ambientales que presenta. Además se han propuesto una serie de adecuaciones de simulación para estimar valores de significancia estadística (Raes and Ter Steege 2007)

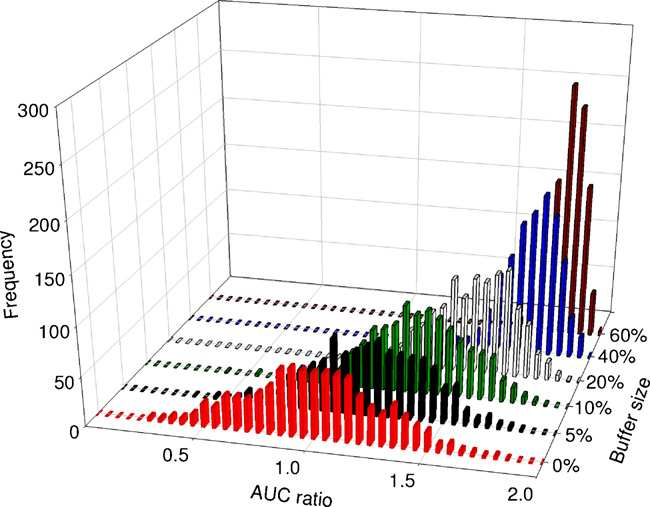
Figura 7.4: Efecto el área de calibración sobre el desempeño predictivo medido con el área bajo la curva.

7.3.1.2 Cociente de áreas parciales

Peterson (Peterson, Papes, and Soberon 2008) propuso una modificación a la AUC llamada ROC parcial, para evaluar predictores espaciales, que están basados en el porcentaje de predicción en relación al tamaño de las áreas predichas al aumentar los umbrales de binarización de un modelo. La diferencia principal entre el cociente de áreas parciales propuesto por Peterson et al. (2008), está en los ejes utilizados para estimarla. En las AUC tradicionales, se utiliza en el eje \(x\) el porcentaje de presencias predichas y en el \(y\) el pocentaje de ausencias clasificadas como presencias. En las ROC parciales, el eje \(x\) es el porcentaje de área predicha y en el \(y\) el porcentaje de presencias predichas (Figura ??).

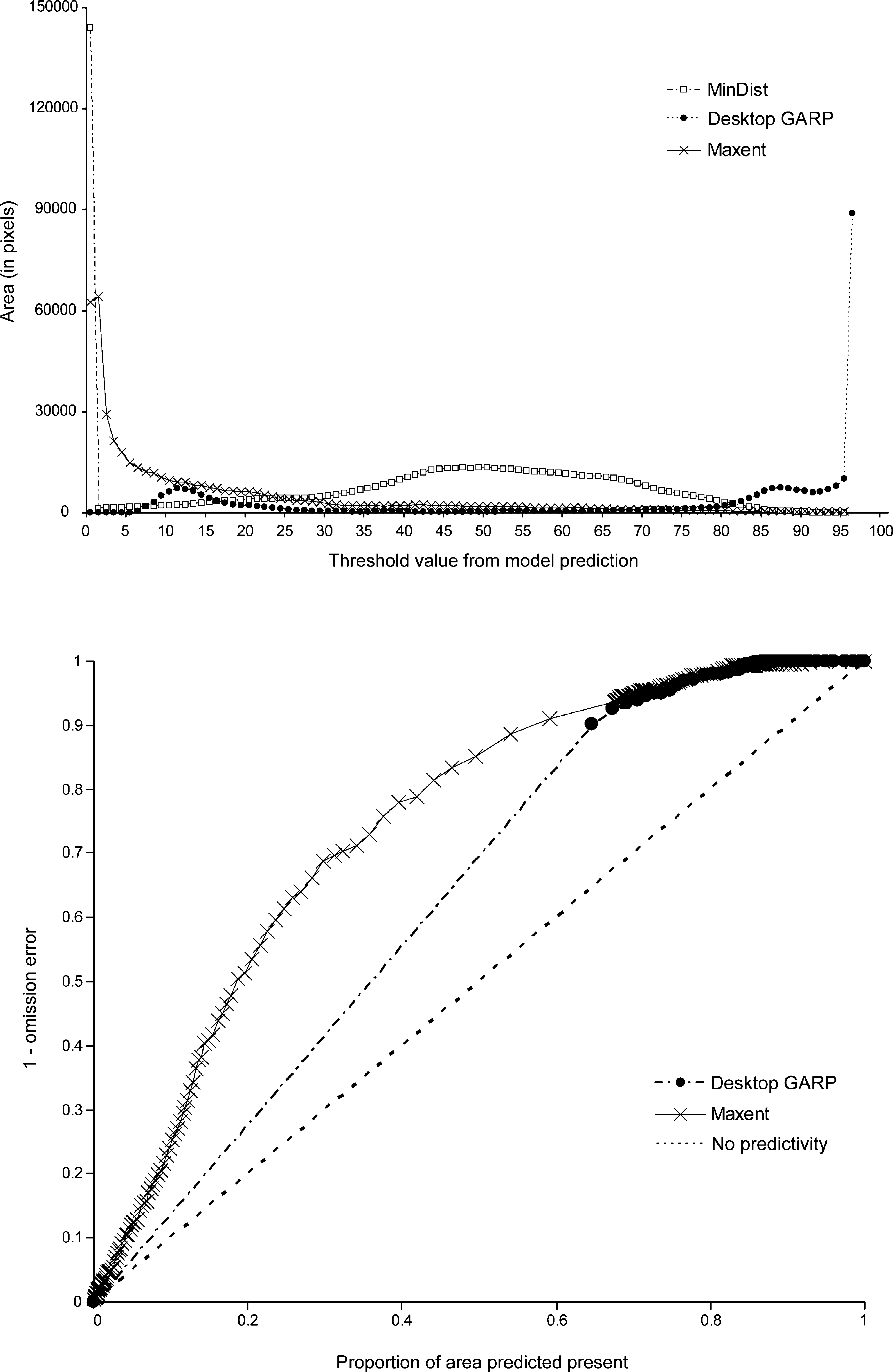
Figura 7.5: Los ejes que utilizados en la estimación de las ROC parciales.

El nombre ROC parcial proviene del hecho de que el valor final obtenido es el cociente del área total bajo la curva entre el área que indica el ubral de predicción aleatoria, que es equivalente a la proporción de área predicha, eliminando posibles sesgos de estimación producto del posible valor que indica predicción aleatoria. Por ejemplo, si un modelo sólo predice 20% del área como favorable para la especie, y en dicha área sólo se encuentra el 20% de las presencias, 20%/20% = 1, lo que indica que el modelo es un predictor netamente aleatorio. Por el contrario, si con un 20% de área predicha, el modelo predice 40% de las presencias 40/20 = 2, indicando que el modelo es significativamente mejor que aleatorio.

El resultado es una métrica de evaluación menos sensible al área de calibración que las AUC tradicionales y que es también más adecuada para evaluar la capacidad predictiva de modelos construidos sólo con datos de presencia (Barve et al. 2011).

7.3.1.3 Tutorial de validación

Vamos a analizar primero dos estrategias de partición de datos, una aleatoria y otra espacialmente estructurada. En la partición aleatoria, los puntos de ajuste y validación se seleccionan aleatoriamente, en la espacialmente estructurada se utilizan todos los puntos de una región para ajustar un modelo y los puntos de otras regiones para validarlo.

7.3.1.3.1 Partición aleatoria

Comenzaremos seleccionanado aleatoriamente el 70% de los puntos para ajuste y 30% para validación, una vez que tengamos el objeto de puntos crudo, sin formatear para spatstat:

datos.aj <- sort(sample(1:nrow(puntos), 0.7 * nrow(puntos)))
datos.val <- c(1:nrow(puntos))[ ! c(1:nrow(puntos))%in% datos.aj ]
write.csv(puntos[datos.val, ], "../Datos-ejemplos/Puntos-validacion.csv", row.names = F)

ppp.aj <- ppp(x = puntos$x[datos.aj], y = puntos$y[datos.aj],
                  window = w)

## Warning: 4 points were rejected as lying outside the specified window

ppp.val <- ppp(x = puntos$x[datos.val], y = puntos$y[datos.val],
                  window = w)

## Warning: 1 point was rejected as lying outside the specified window

En datos.aj estamos seleccionando al azar las filas para ajustar el modelo, mientras que en datos.val, estamos extrayendo todas las filas que no se seleccionaron para ajustar. Una vez identificados los puntos que se utilizarán para ajustar y validar, se utilizan los índices para crear los dos objetos que se utilizarán para ajustar y validar respectivamente. El procedimiento para ajustar un modelo con la base de datos de ajuste es el mismo que anteriormente. Nos saltamos la parte del diagnóstico pues el interés ahora se centra en medir la capacidad predictiva. Una vez ajustado el modelo necesitamos guardar las predicciones en formato raster

m.val <- ppm(Q = ppp.aj, # Proceso de puntos en formato ppp
             trend = ~ Var.2 + Var.3 + I(Var.2^2) + I(Var.3^2), #  Formula del modelo seleccionado     
             covariates = s.im)
pred.val <- predict(m.val, dimyx = c(28, 30), type = "trend")
pred.val.r <- raster(pred.val)
writeRaster(pred.val.r, "../Datos-ejemplos/Res/Predicciones-validacion-aleat", "GTiff", overwrite = T)

Una vez guardadas las predicciones del modelo, necesitamos instalar y cargar el paquete kuenm que contiene la función para calcular las ROC parciales. La instalación es un poco diferente pues requiere instalar el paquete devtools porque kuenm no está almacenado en los repositorios de R.

devtools::install_github("marlonecobos/kuenm")

Una vez, instalado, continuamos evaluando el modelo con el cociente de áreas del ROC:

puntos.val <- read.csv("../Datos-ejemplos/Puntos-validacion.csv")
model <- raster("../Datos-ejemplos/Res/Predicciones-validacion.tif")
proc <- kuenm::kuenm_proc(occ.test = puntos.val,
                  model = model,
                  threshold = 5,
                  rand.percent = 50,
                  iterations = 39, parallel = F)

## Warning: `mutate_()` was deprecated in dplyr 0.7.0.
## ℹ Please use `mutate()` instead.
## ℹ See vignette('programming') for more help
## ℹ The deprecated feature was likely used in
##   the dplyr package.
##   Please report the issue at
##   <]8;;https://github.com/tidyverse/dplyr/issueshttps://github.com/tidyverse/dplyr/issues]8;;>.

para ver los resultados:

proc$pROC_summary

## Mean_AUC_ratio_at_5%            pval_pROC 
##             1.051373             0.000000

7.3.1.4 Datos de validación estructurados espacialmente

Para muestrear los puntos con una estructura espacial, necesitamos diseñar un criterio. Una de las alternativas más populares es la creación de una cuadrícula de ajedrez, y utilizar los puntos en cuadros blancos para ajustar y los puntos en cuadros negros para validar. La generación de los cuadros está implementada en el paquete dismo, en la función gridSample:

p.bl <- dismo::gridSample(puntos, r = s[[1]], n = 50, chess = "white")
p.ne <- dismo::gridSample(puntos, r = s[[1]], n = 50, chess = "black")

Como muestra del resultado:

plot(s[[1]]); points(p.bl)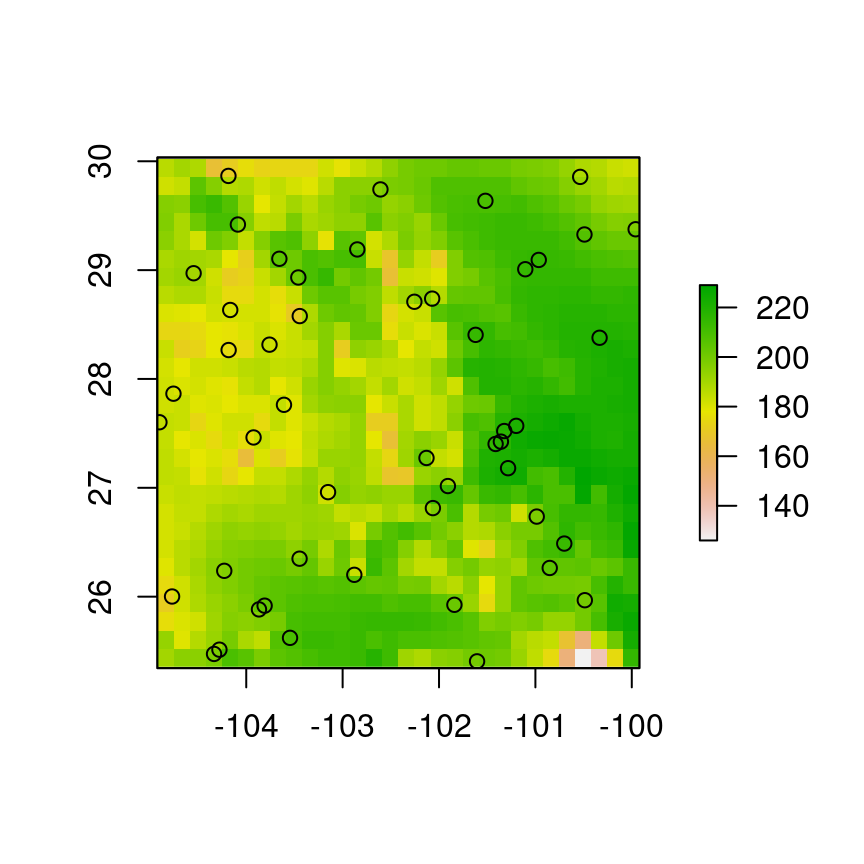

plot(s[[1]]); points(p.ne)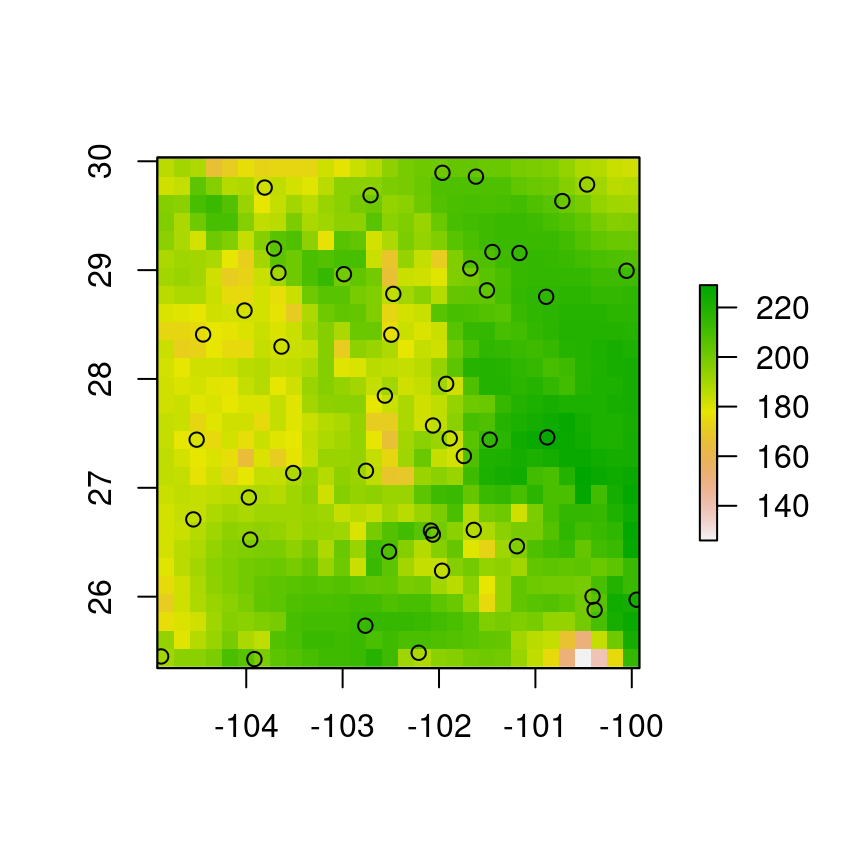

A partir de este punto el proceso de validación es el mismo que con las muestras aleatorias, aunque es preferible seguir el siguiente proceso:

1. Ajustar modelo con puntos en cuadrantes blancos y validar con puntos en cuadrantes negros
2. Ajustar modelo con puntos en cuadrantes negros y validar con puntos en cuadrantes blancos

References

Barve, Narayani, Vijay Barve, Alberto Jiménez-Valverde, Andres Lira-Noriega, Sean P Maher, a. T Peterson, Jorge Soberón, and Fabricio Villalobos. 2011. “The Crucial Role of the Accessible Area in Ecological Niche Modeling and Species Distribution Modeling.” Ecological Modelling 222 (11): 1810–19. https://doi.org/10.1016/j.ecolmodel.2011.02.011.

Peterson, A Townsend, Monica Papes, and Jorge Soberon. 2008. “Rethinking Receiver Operating Characteristic Analysis Applications in Ecological Niche Modeling.” Ecological Modelling 213 (1): 63–72. https://doi.org/10.1016/j.ecolmodel.2007.11.008.

Raes, Niels, and Hans Ter Steege. 2007. “A Null-Model for Significance Testing of Presence-Only Species Distribution Models.” Ecography 30 (5): 727–36. https://doi.org/10.1111/j.2007.0906-7590.05041.x.

Renner, Ian W, and David I Warton. 2013. “Equivalence of MAXENT and Poisson Point Process Models for Species Distribution Modeling in Ecology.” Biometrics 69 (1): 274–81. https://doi.org/10.1111/j.1541-0420.2012.01824.x.

Velasco, Julián A, and Constantino González-Salazar. 2019. “Akaike Information Criterion Should Not Be a ‘Test’ of Geographical Prediction Accuracy in Ecological Niche Modelling.” Ecological Informatics 51: 25–32.