5 Unidad III: Introducción al cálculo diferencial e integral

5.1 Sucesiones

En matemáticas, de manera muy general, las sucesiones pueden ser entendidas como una función cuyo dominio siempre es el conjunto o un subconjunto de los números naturales, mientras que el codominio puede pertenecer a cualquier otro conjunto. En notación tradicional de funciones tenemos entonces que \(x \in \mathbb{N}\), mientras que:

\[\begin{equation} y(x) \in \begin{cases}\mathbb{R}\\ \mathbb{Z}\\ \mathbb{N} \end{cases} \end{equation}\]

La mayoría de las sucesiones, sin embargo que se utilizan en ecología, corresponden a:

\[\begin{equation} f: \begin{aligned}[t] \mathbb{N}_0 \rightarrow \mathbb{R} \\ n \rightarrow f(n) \end{aligned} \end{equation}\]

una función \(f\) de los números naturales, incluido el cero (\(\mathbb{N}_0\)) que produce números reales (\(\mathbb{R}\)), cuyo dominio es \(n\), y codominio es \(f(n)\).

Otra característica de las sucesiones es que sus elementos están ordenados, es decir, cada elemento en el dominio y codominio tiene un sitio particular, de modo que si los conjuntos \(a_n = \{A, B, C\}\) y \(a_m = \{C, A, B\}\), \(a_n \neq a_m\), puesto que, aunque contengan los mismos elementos \(A, B\) y \(C\), estos tienen posiciones diferentes dentro de \(a_n\) y \(a_m\).

5.1.1 Notación de sucesiones

Una sucesión de los números naturales suele nombrarse como \(\{a_n\}\), seguida de la regla de correspondencia entre el conjunto \(n\) y \(a\). Así por ejemplo:

\[\begin{equation} \{a_n\} = 2n \tag{5.1} \end{equation}\]

es una sucesión de los números naturales pares, tal que:

\[a_1 = 1, a_2 = 4, a_3 = 6, a_4 = 8 \dots\] Esta notación, sin embargo no es universal, por ejemplo:

-\((a_n) = a_1, a_2, a_3, \dots\)

-\((a_k)_{k=1}^m = a_1, a_2, a_3, \dots, a_m\)

-\(\{a_n\}_{n \in \mathbb{N}} = a_1, a_2, a_3, \dots\)

5.1.2 Tipos de sucesiones

La sucesión anterior es un ejemplo muy sencillo y poco útil en la modelación ecológica, pero es un punto de partida para entender la notación y el concepto. Existen sucesiones, sin embargo, que tienen implicaciones importantes para el desarrollo de modelos dinámicos, como las sucesiones por recurrencia.

5.1.2.1 Sucesiones recurrentes

En estas sucesiones, la regla de correspondencia indica algún tipo de operación con elementos de \(n\) en posiciones previas. Así por ejemplo, la sucesión:

\[\begin{equation} \{a_n\} = a_{n-1} + a_{n-2} \tag{5.2} \end{equation}\]

se conoce como sucesión de Fibonacci, en la que, el elemento \(n\) se obtiene sumando los elementos \(n-1\) y \(n-2\) de la secuencia \(\{a_n\}\).

Tabla 5.1: Secuencia de Fibonacci para los diez primeros números naturales.

n	a
1	1
2	1
3	2
4	3
5	5
6	8
7	13
8	21
9	34
10	55

La secuencia de finonacci, tiene un comportamiento parecido a la función exponencial, en el sentido de que el crecimiento de \(a\) es más rápido conforme los valores de \(a\) son mayores.

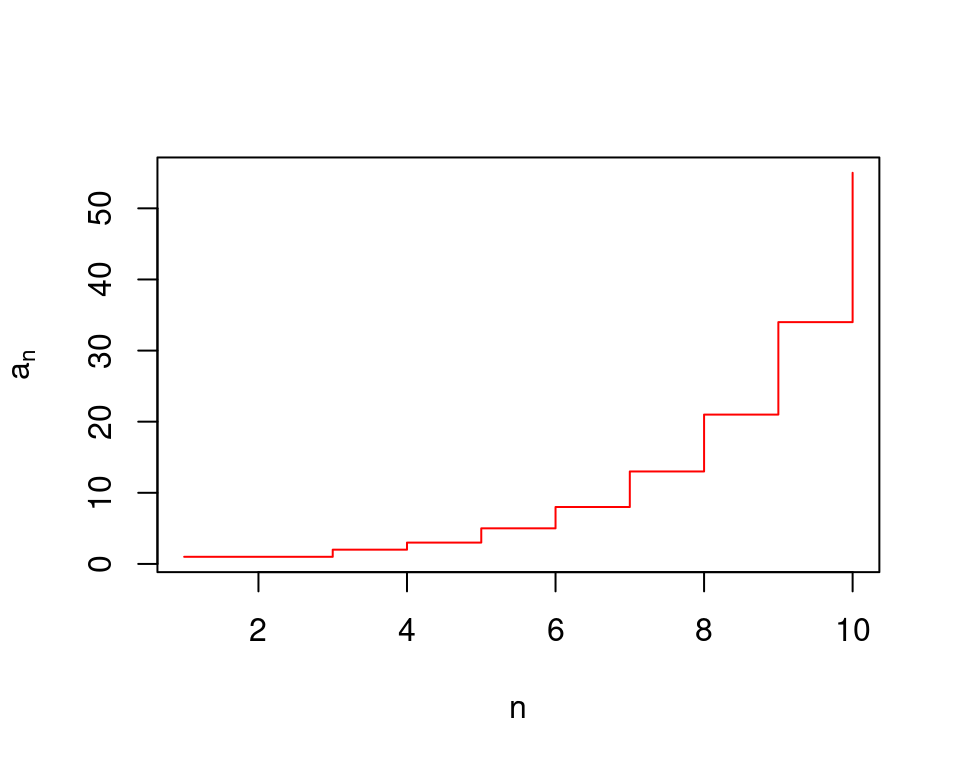
Figura 5.1: Representación gráfica de la secuencia de Fibonacci.

5.1.2.2 Sucesiones recurrentes más avanzadas

Las sucesiones recurrentes pueden ser también concebidas como modelos dinámicos en tiempo discreto, donde el tiempo está representado por el conjunto de los números naturales, así, por ejemplo, el crecimiento de una población lo podemos representar como:

\[\begin{equation} N_{t} = r N_{t-1} \tag{5.3} \end{equation}\]

Como podemos ver, en (5.3), el crecimiento por unidad de tiempo es lineal con respecto del número de individuos en el periodo de tiempo inmediatamente previo (\(rN_{t-1}\)).

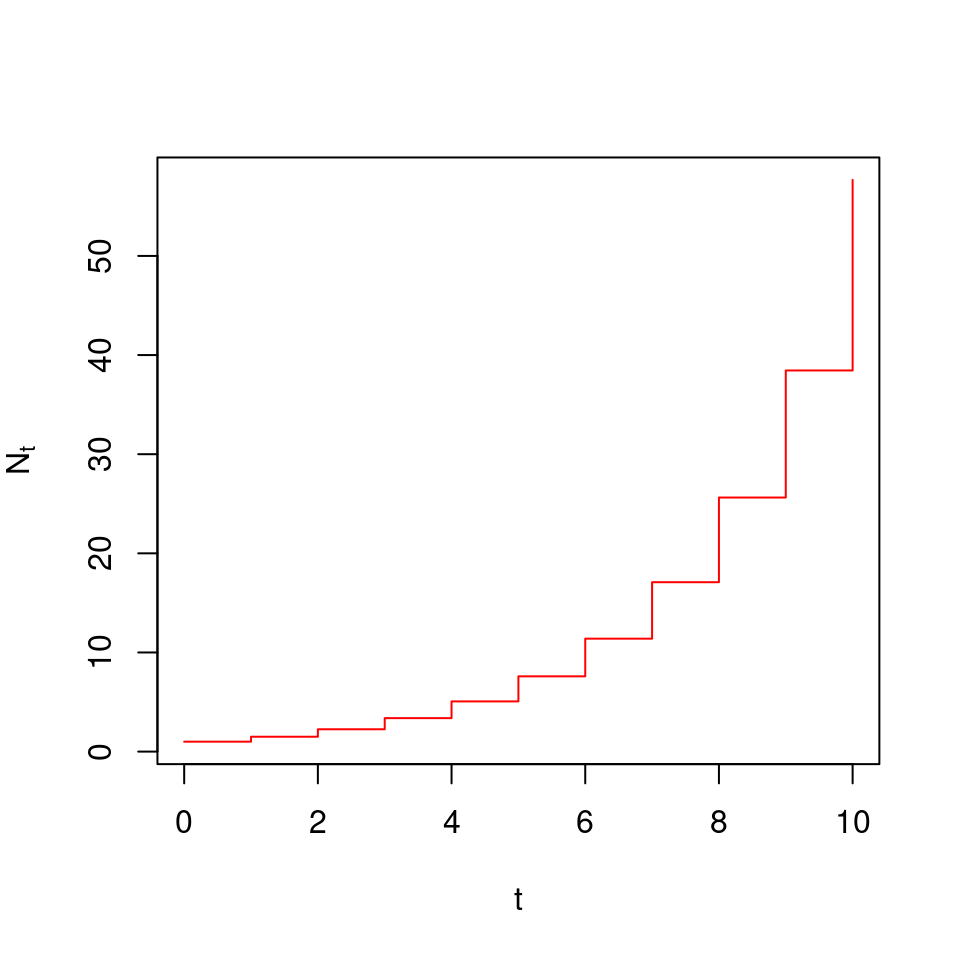
Figura 5.2: Simulación de la sucesión de crecimiento poblacional en tiempo discreto, para 10 unidades de tiempo, con r = 1.5, y una población inicial de N = 1.

La sucesión descrita por la ecuación (5.3) es fácil de simular con una computadora, con aplicaciones tan populares como las hojas de cáculo como excel.

Con este tipo de sucesiones, es posible comenzar a utilizar conceptos básicos de cálculo. Podemos por ejemplo, tomar la misma sucesión de la ecuación (5.3), con una población inicial de \(N = 50\), y \(r = 0.6\), y simular por un periodo de tiempo de 20, para ver hacia qué valor se aproxima \(N_t\) (5.3).

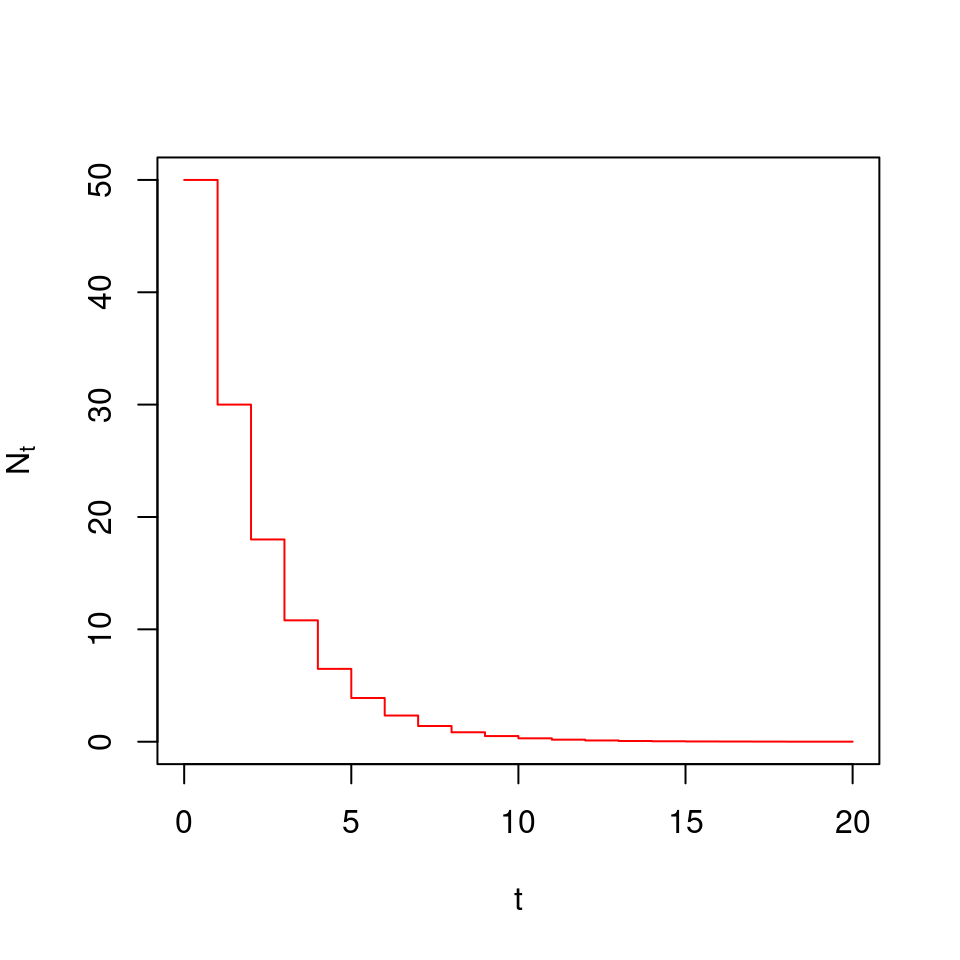
Figura 5.3: Simulación para un valor inicial de N = 50, por 20 unidades de tiempo, y r = 0.6

En cada simulación, \(N_t\) cambia de acuerdo con el valor de \(N_{t-1}\). Como es evidente, si \(r > 1\), \(N_t\) crece, y mientras \(t \rightarrow \infty\), \(N_t \rightarrow \infty\). En el caso contrario, cuando \(r < 1\) y \(t \rightarrow \infty\), \(N_t \rightarrow 0\)

En estos casos, decimos que por ejemplo para \(r < 1\), \(N\) está acotada por \(0\). Hay otras sucesiones, por ejemplo la de crecimiento logístico, que está acotada por la capacidad de carga, incluso si \(r > 0\).

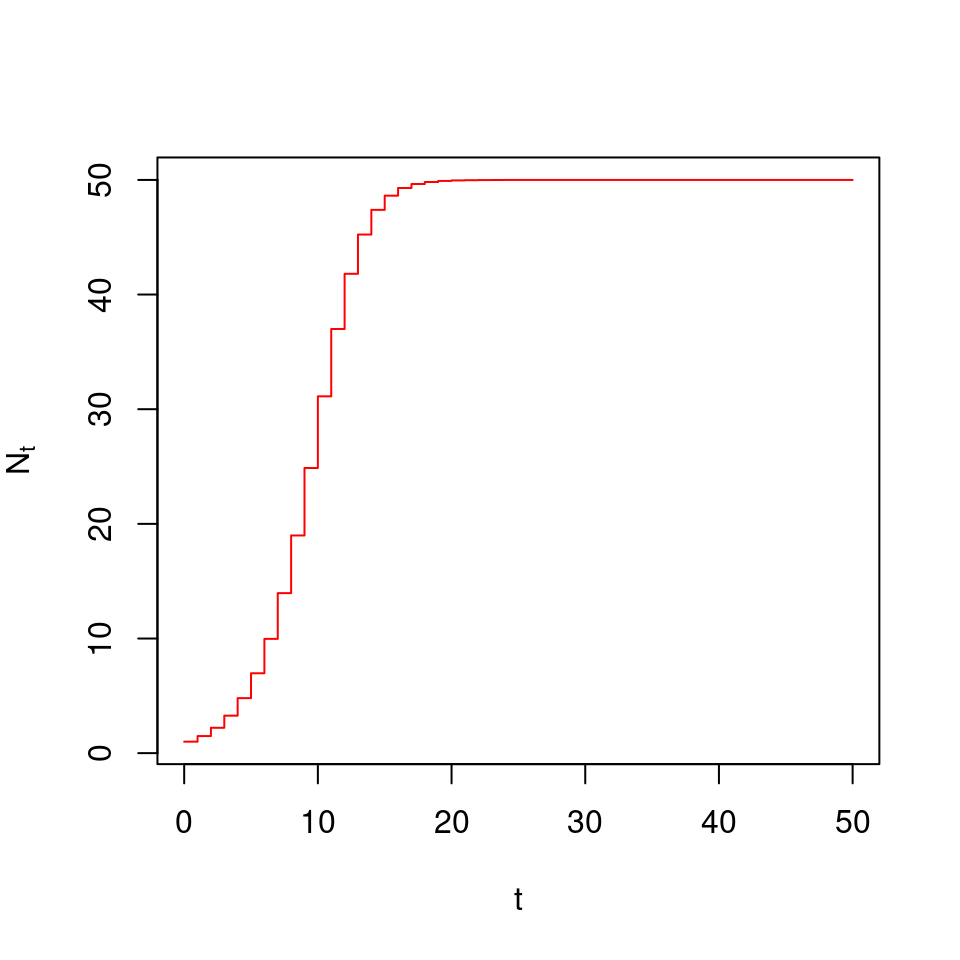
Figura 5.4: Simulación para un valor inicial de N = 1, por 50 unidades de tiempo, r = 0.5, y capacidad de carga K = 50

La sucesión para el crecimiento logístico en tiempo discreto es:

\[\begin{equation} N_{t} = N_{t-1} + r N_{t-1} \left(1 - \frac{N_{t-1}}{K} \right) \tag{5.4} \end{equation}\]

5.1.2.3 Ejercicio

Utilizando la hoja de cálculo para la sucesión de crecimiento poblacional en tiempo discreto, adaptala para simular el crecimiento poblacional probando los valores de \(r\) dese 0.5 hasta 3.5 en incrementos de 0.25, y grafícalos. ¿Qué pasa con \(N_t\) con los valores de \(r\) probados?

5.2 Continuidad y límites

La continuidad y los límites son la puerta de entrada a la derivación y por lo tanto a las ecuaciones diferenciales. Cuando decimos que una función es contínua en un intervalo definido del dominio \((x_1, x_2)\), quiere decir que \(f(x)\) está definida para todos y cada uno de los posibles valores de \(x\) en ese intervalo. Existen muchas funciones que no son contínuas, por ejemplo:

\[\begin{equation} f(x) = \frac{x - 1}{x - 1} \tag{5.5} \end{equation}\]

Como es evidente, dicha ecuación está definida para todos los valores posibles de \(x\), excepto \(x = 1\), porque \(f(1) = \frac{1 - 1}{1-1} = \frac{0}{0}\), lo cual es una indeterminación, no existe.

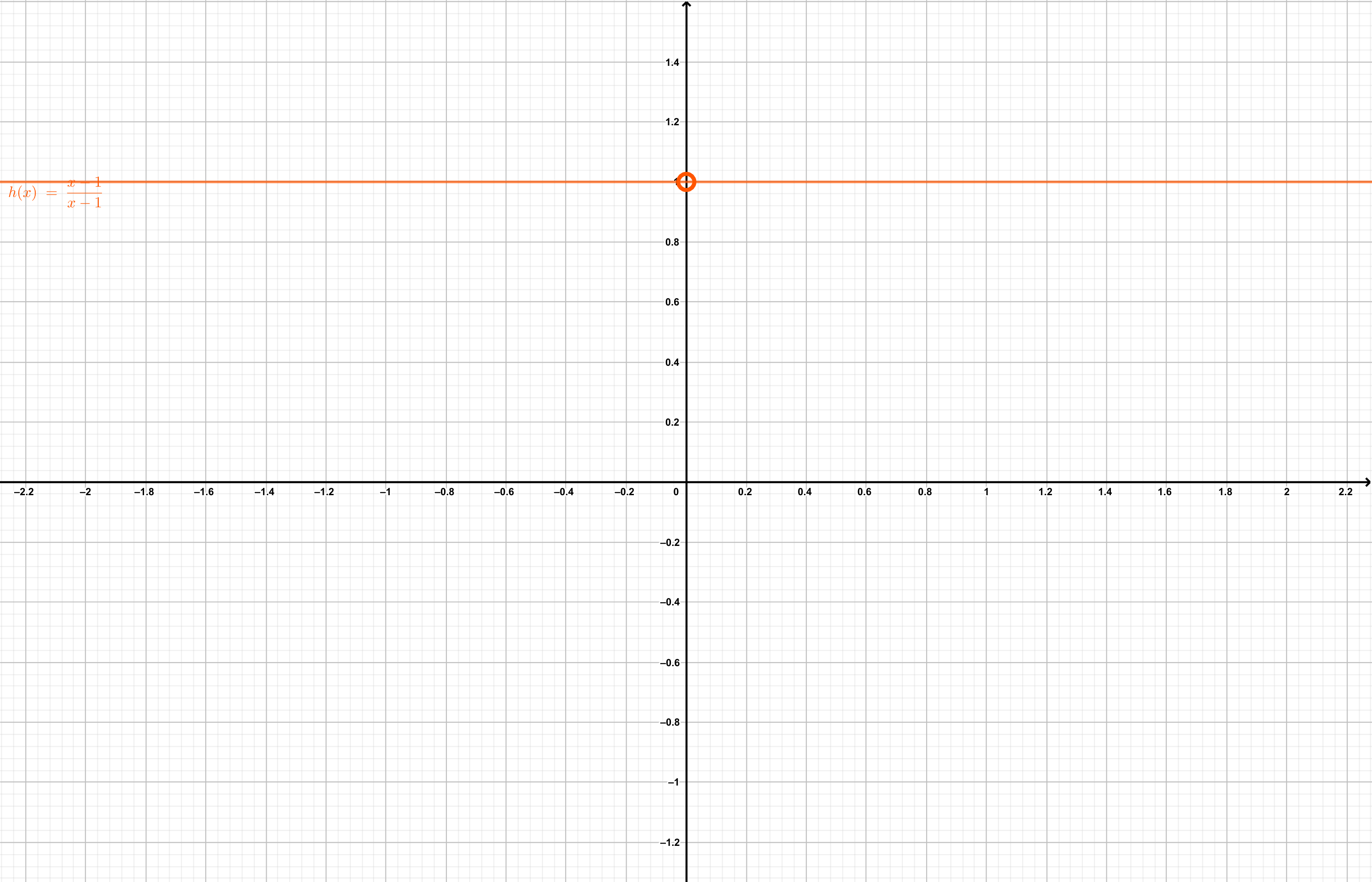
Figura 5.5: Ejemplo de función con discontinuidad.

Hay funciones con discontinuidades, gráficamente más evidentes que (5.5), como la hipérbola, \(f(x) = 1/x\) (figura 5.6) o \(g(x) = |x|/x\), o aquellas con condicionales.

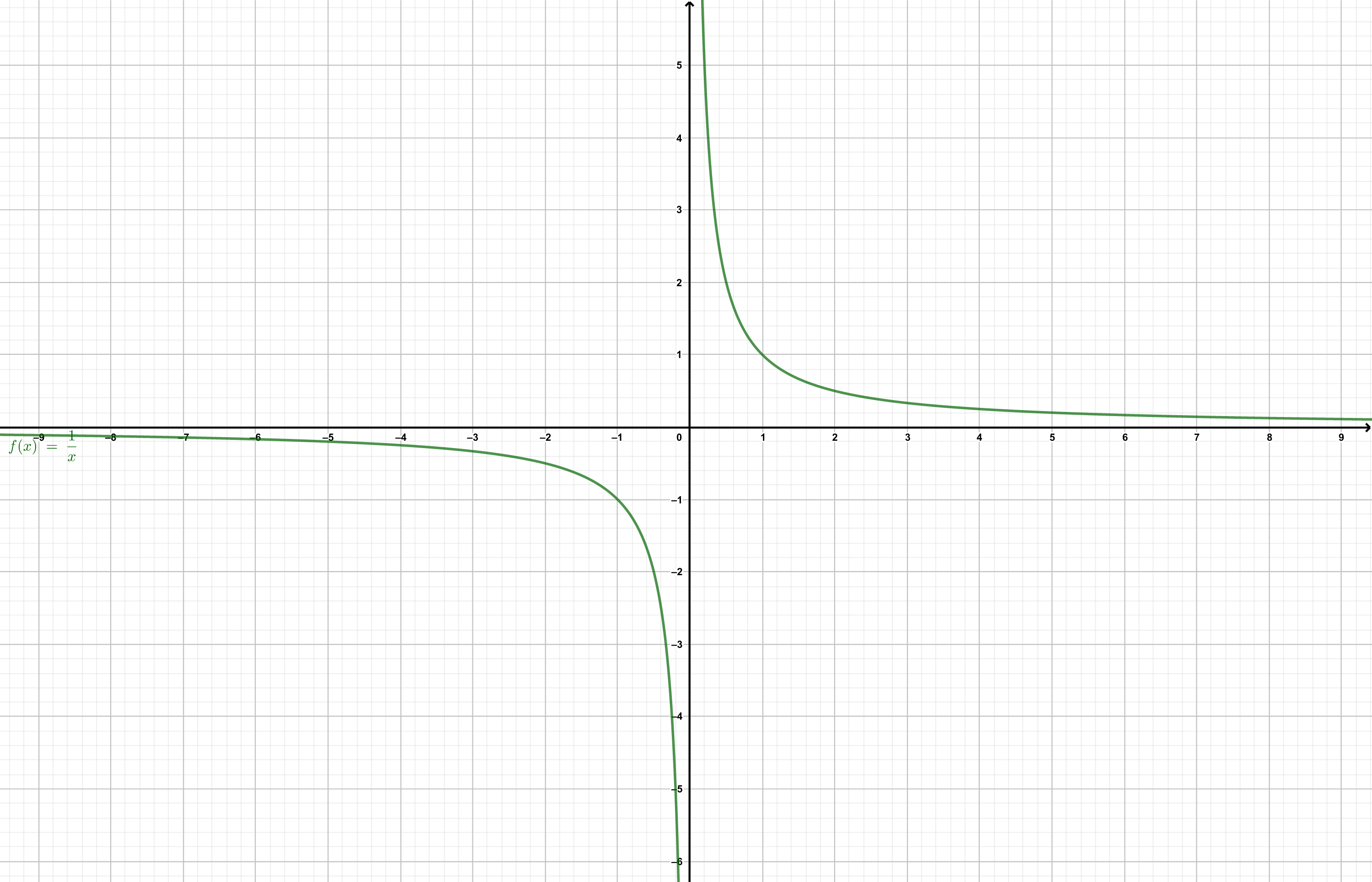
Figura 5.6: La hipérbola.

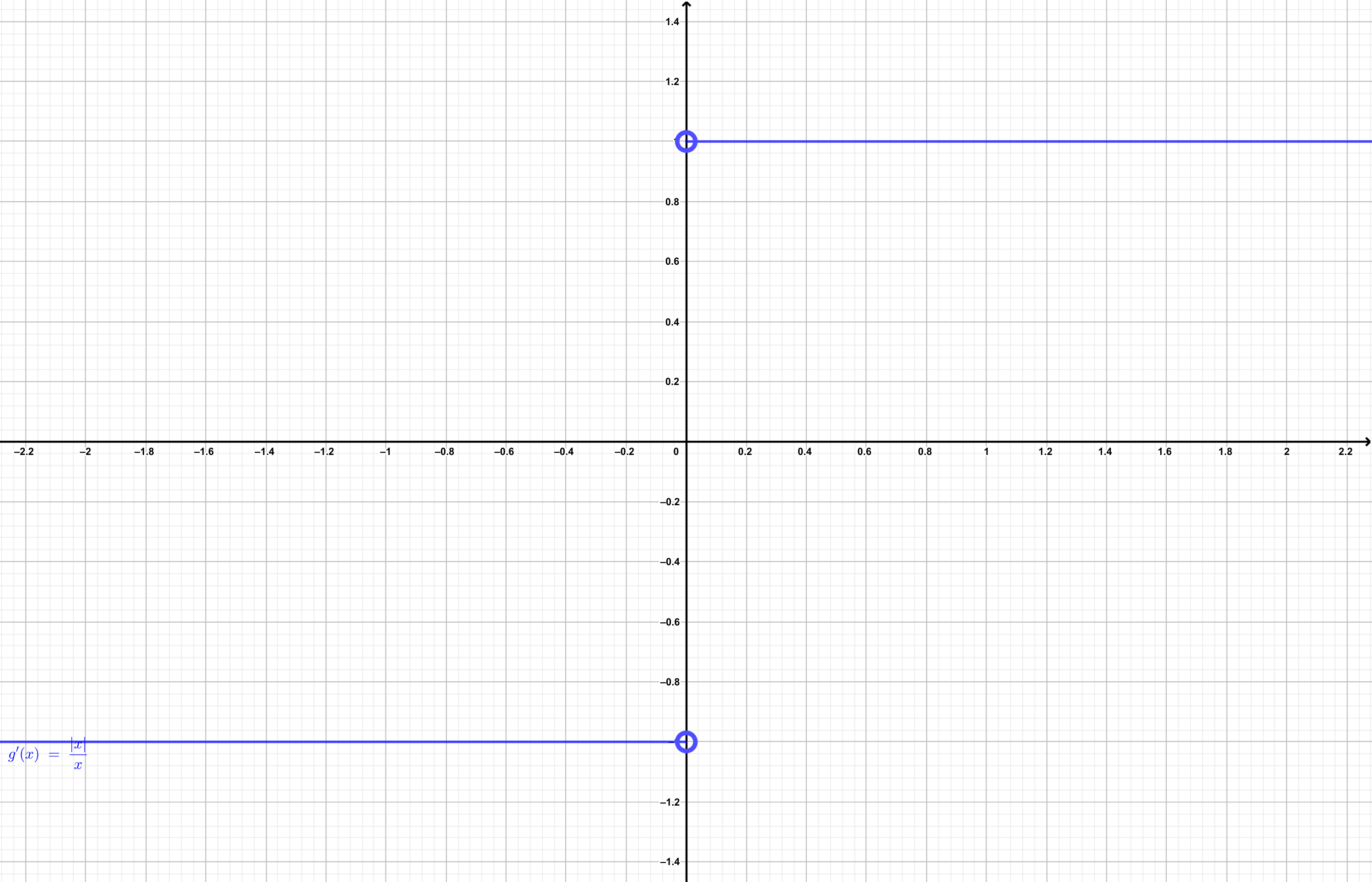
Figura 5.7: Cociente de valor absoluto.

Como resulta geométricamente evidente, todas estas funciones son discontínuas para algún valor de \(x\), sin embargo existe una diferencia muy importante entre ellas y es que el valor que pueden tomar en torno al punto en que son discontínuas depende de qué lado nos acerquemos a este punto. Para la equación \(f(x) = \frac{x-1}{x-1}\), resulta claro que si nos acercamos a \(f(1)\) desde un valor \(x>1\), llegamos a un valor similar de \(f\) que si nos acercamos a \(f(1)\) por medio de un valor de \(x < 1\). Esto no sucede con las función \(g(x) = |x|/x\) puesto que si nos acercamos a \(g(0)\) por el lado positivo de \(x\) nos acercamos a \(g = 1\), mientras que, por el lado negativo, nos acercamos a \(g = -1\).

En este momento entonces es necesario comenzar a hablar del concepto de límite.

5.2.1 El límite

En el sentido estricto de la palabra, límite es el valor al que se acerca una función para un valor específico del dominio. En matemáticas, existe una notación específica para decir esto:

\[\begin{equation} \lim \limits_{x \rightarrow a} x + 1 \end{equation}\]

donde \(\lim\) indica que necesitamos estimar el límite de la función, cuando su dominio \(x\) toma valores cada vez más cercanos a algún valor específico \(a\) (\(x \rightarrow a\)). Aquí es necesario especificar que cuando hablamos de límites siempre nos acercamos al valor de interés \(a\) tanto por medio de valores de \(x>a\) como \(x<a\), es decir alrededor de un intervalo de valores de \(x\) que comunmente se denomina como \(a \pm \delta\). Entonces, el límite de \(f(x)\) existe si todos los valores de \(f(a \pm \delta)\) convergen alrededor de un mismo punto.

Revisa la aplicación de Geogebra Límites para visualizar este fenómeno. Juega con los valores de \(\delta\) y \(a\) para ver cómo están definidos los valores de la función alrededor de \(a\) para la función de la línea recta. Posteriormente, cambia la ecuación por:

1. \(f(x) = \frac{|x|}{x}\)
2. \(f(x)= \frac{1}{x}\)

para examinar qué pasa con \(f(x)\) cuando \(x \rightarrow 0\)

En los casos en que los valores de \(f(x)\) tienden a un valor único para \(f(a + \delta)\) y \(f(a - \delta)\), el límite de la función sí existe (figura 5.5). En cambio, como ocurre para funciones como \(1/x\) y \(|x|/x\), existe más de un valor al que ambas funciones se aproximan (figuras 5.6 y 5.7) dependiendo se si se evalúa \(f(a + \delta)\) ó \(f(a - \delta)\), el límite no existe.

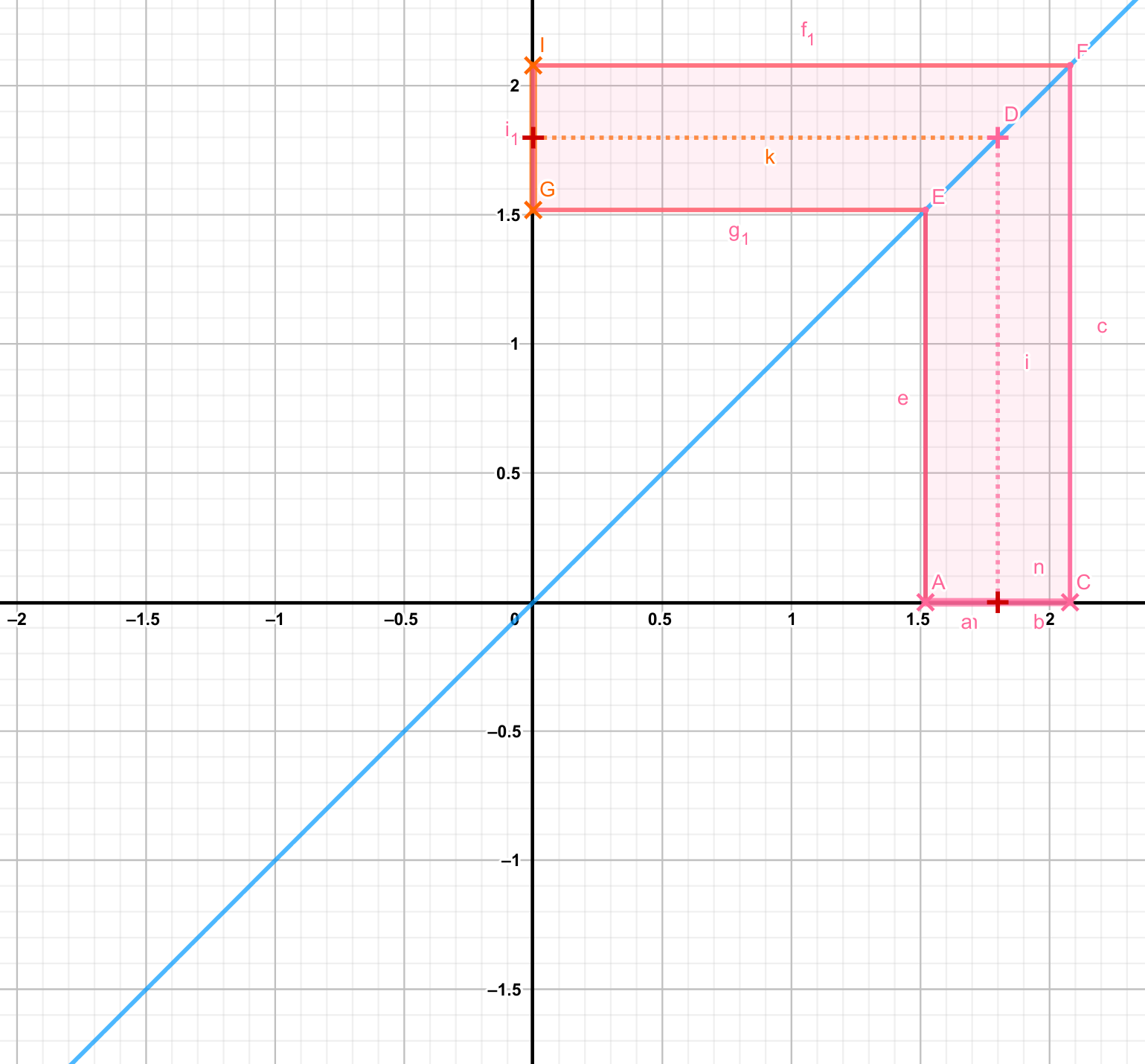
Figura 5.8: Ejemplo gráfico de una función con límite definido para cualquier valor de \(x\). El valor \(a\) al que \(x\) se aproxima está marcado en el eje \(x\) con una cruz roja, y el tamaño de ð alrededor de \(a\) está delimitado con las marcas rosas. Nota cómo todos los valores posibles de \(f(x)\) alrededor de \(f(a)\) convergen en el mismo punto correspondiente a \(f(a)\).

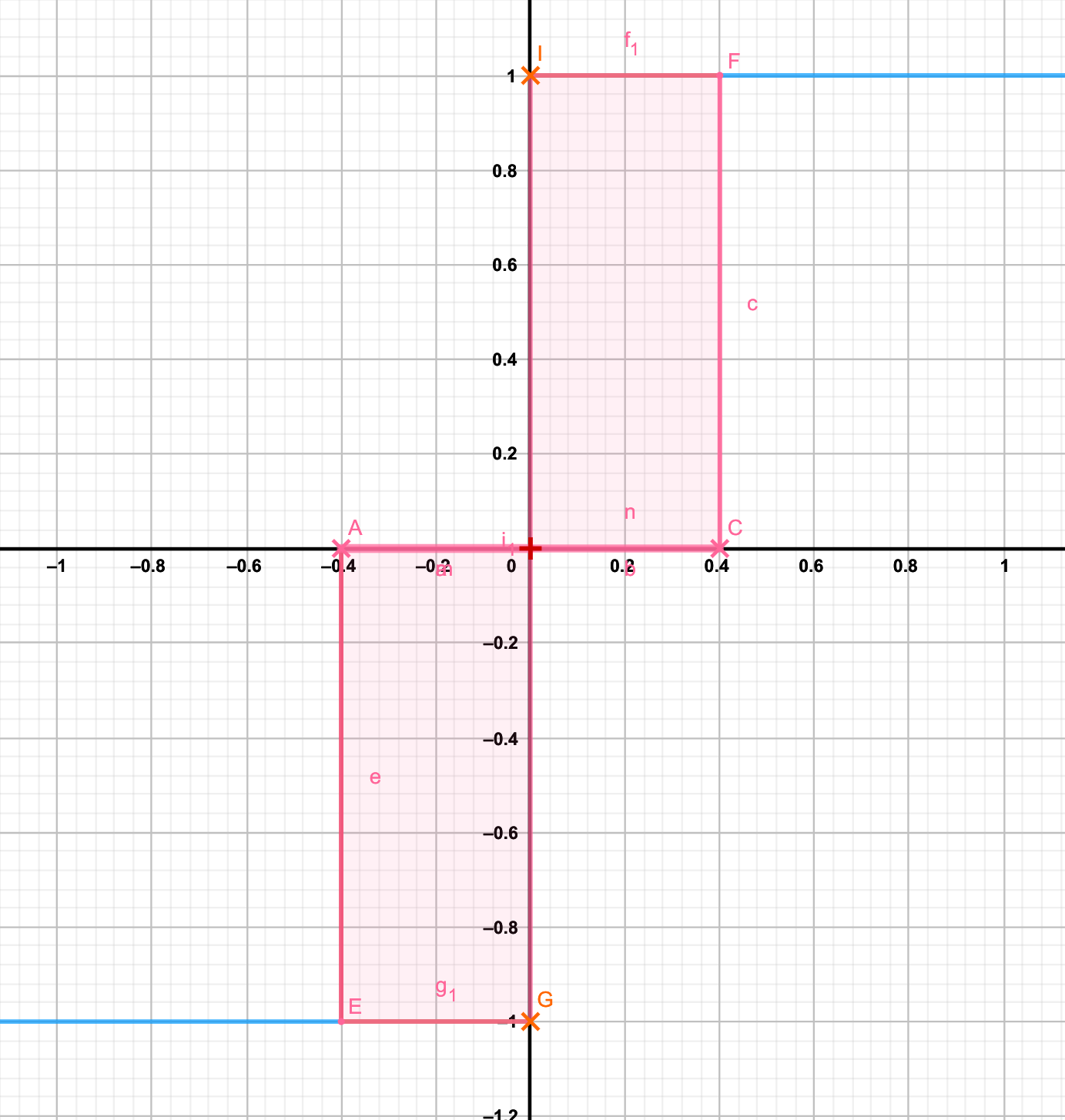
Figura 5.9: Ejemplo gráfico de una función sin límite definido cuando x→0 (equis tiende a cero). Nota cómo hay dos valores posibles a los que la función se acerca cuando x→0, ya sea cuando uno se acerca a 0 por el lado positivo de \(x\) o el lado negativo de \(x\).

Aún cuando estas funciones no satisfacen la definición estricta de límite, es posible encontrar los límites de la función para \(f(a)\), dependiendo del lado por el que \(x \rightarrow a\). Veamos el ejemplo de \(f(x) = |x|/x\) dado en la figura 5.9. El límite que nos interesa es

\[ \lim \limits_{x \rightarrow 0} \frac{|x|}{x}\] Por lo que sabemos hay dos maneras que acercarnos a \(0\), una por el lado positivo, \(x \rightarrow 0^{+}\), y otra por el lado negativo \(x \rightarrow 0^-\). Así entonces podemos establecer dos límites:

1. \(\lim \limits_{x \rightarrow 0^+} \frac{|x|}{x} = 1\)
2. \(\lim \limits_{x \rightarrow 0^-} \frac{|x|}{x} = -1\)

5.2.1.1 ¿Cómo se encuentran los límites?

Enncontrar límites puede ser problemático, por lo que existe una variedad de estrategias cuyo uso depende del tipo de expresión que estemos evaluando. Por lo general, si tenemos \(\lim\limits_{x \rightarrow a} f(x)\) se puede comenzar por evaluar \(f(a)\), con lo que tenemos tres posibilidades:

1. \(f(a) = \frac{b}{0}, b \neq 0\) (una asíntota vertical como en \(1/x\))
2. \(f(a) = b\) (límite encontrado)
3. \(f(a) = \frac{0}{0}\) (indeterminación)

En el caso 1, es probable que el límite no exista, lo cual depende de que \(\lim\limits_{x \rightarrow a^-} f(x) = \lim\limits_{x \rightarrow a^+} f(x)\). Para el caso 2, el límite está claramente definido y no hay mayor problema. En el caso 3, es necesario encontrar una manera equivalente de representar a \(f(a)\).

5.2.1.2 Representación equivalente de las funciones

Las tres estrategias más comunes para resolver límites donde \(f(a) = \frac{0}{0}\) son:

1. Factorizar \(f(a)\)
2. Conjugar \(f(a)\)
3. Usar identidades trigonométricas

Cabe aclarar que muchas de las transformaciones aquí descritas surten efecto bajo el supuesto de que \(x \neq a\), aunque una vez transformadas las funciones en efecto las evaluamos asumiendo que \(x = a\). Con esto en mente veamos un ejemplo para cada estrategia.

5.2.1.2.1 Factorización

Factorizar consiste en representar un polinomio como una serie de productos de binomios (generalmente). Así, por ejemplo:

\[\begin{equation} \lim \limits_{x \rightarrow -3} \frac{x^2 + x -6}{x + 3} \end{equation}\]

por sustitución directa tenemos que

\[\begin{equation} \frac{(-3)^2 - 3 - 6}{-3 + 3} = \frac{0}{0} \end{equation}\]

Y una vez factorizado, asumiendo que \(x \neq 3\) tenemos

\[\begin{equation} \frac{x^2 + x - 6}{x + 3} = \frac{(x + 3)(x - 2)}{x + 3} = x-2 \end{equation}\]

por lo tanto, utilizando sustitución directa en la forma factorizada tenemos que:

\[\begin{equation} \lim\limits_{x \rightarrow 3} x - 2 = - 3 - 2 = -5 \end{equation}\]

5.2.1.2.2 Conjugación racional

Una expresión conjugada de un binomio está basada en la identidad:

\[ a^2 - b^2 =(a + b)(a - b)\]

Esta identidad se puede extender a los radicales:

\[ a - b = (\sqrt{a} + \sqrt{b})(\sqrt{a} - \sqrt{b})\]

De modod que el conjugado de \(a + b\) es \(a-b\), y el de \(\sqrt{a} + \sqrt{b}\) es \(\sqrt{a} - \sqrt{b}\).

La aplicación de conjugados entonces es particularmente útil cuando queremos evaluar un el límite de una funcion racional con radicales. Por ejemplo en:

\[\begin{equation} \lim \limits_{x \rightarrow 0} \frac{\sqrt{1 + x}-1}{x} \end{equation}\]

por sustitución directa obtenemos , pero no es posible factorizar el numerador, por lo tanto podemos utilizar el conjugado de \(\sqrt{1 + x} - 1\). La manera de hacerlo es, primero identificar el cojugado como:

\[\begin{equation} \sqrt{1 + x} + 1 \end{equation}\]

Y multiplicar tanto el nuemerados como denominador por el conjugado:

\[\begin{equation} \frac{\sqrt{1 + x}-1}{x} \cdot \frac{\sqrt{1 + x} + 1}{\sqrt{1 + x} + 1} = \frac{1 + x-1}{x(\sqrt{1 + x} + 1)} = \frac{1}{\sqrt{1 + x} + 1} \end{equation}\]

Con lo que ya podemos evaluar:

\[\begin{equation} \lim\limits_{x \rightarrow 0} \frac{1}{\sqrt{1 + x} + 1} = \frac{1}{1 + 1} = \frac{1}{2} \end{equation}\]

5.2.1.2.3 Identidades trigonométricas

Cuano es necesario evaluar el límite de una función trigonométrica, es útil echar mano de las identidades, además de las ya bien conocidas, las pitagóricas:

1. \(\mathrm{sen}^2 \theta + \cos^2 \theta = 1\)
2. \(\sec^2 \theta - \tan^2 \theta = 1\)
3. \(\csc^2 \theta - \cot^2 \theta = 1\)

Comencemos por ver un ejemplo basado en las identidades basadas en los cocientes.

\[\begin{equation} \lim \limits_{x \rightarrow 0} \frac{3x \tan x}{\mathrm{sen}x} \end{equation}\]

por sustitución directa tenemos que:

\[\begin{equation} \frac{3(0)\tan 0}{\mathrm{sen} 0} = \frac{0}{0} \end{equation}\]

lo que indica que necesitamos representar a la función de una manera alternativa, echando mano de las identidades. Sabemos que:

\[\begin{equation} \tan \theta = \frac{\mathrm{sen} \theta}{\cos \theta} \end{equation}\]

por lo tanto podemos representar la función como:

\[\begin{equation} \frac{3x \tan x}{\mathrm{sen}x} = \frac{3x \mathrm{sen} x}{\cos^2 x} = \frac{3x}{\cos x} \end{equation}\]

Entonces, tenemos el límite que puede ser evaluado por sustitución directa:

\[\begin{equation} \lim \limits_{x \rightarrow 0} \frac{3x}{\cos x} = \frac{3(0)}{\cos 0} = \frac{0}{1} = 0 \end{equation}\]

5.2.1.3 Equivalencias de límites

Los límites, como hemos visto, son números reales, por lo que todos los axiomas que ya conocemos aplican a los números reales:

1. \(\lim \limits_{x \rightarrow a} f(x) + g(x) = \lim \limits_{x \rightarrow a} f(x) + \lim \limits_{x \rightarrow a} g(x)\)

2. \(\lim \limits_{x \rightarrow a} f(x) \cdot g(x) = \lim \limits_{x \rightarrow a} f(x) \cdot \lim \limits_{x \rightarrow a} g(x)\)

3. \(\lim \limits_{x \rightarrow a} \frac{f(x)}{g(x)} = \frac{\lim \limits_{x \rightarrow a} f(x) }{ \lim \limits_{x \rightarrow a} g(x)}\)

4. \(\lim \limits_{x \rightarrow a} c f(x) = c \lim \limits_{x \rightarrow a} f(x)\)

5. \(\lim \limits_{x \rightarrow a} f(x)^2 = \left( \lim \limits_{x \rightarrow a} f(x) \right)^2\)

5.3 Derivación

Hasta el momento hemos mencionado en repetidas ocasiones una serie de conceptos relacionados muy íntimamente con la derivación. En esencia, en cálculo, el proceso de derivación se utiliza para estimar la pendiente de una recta tangente a un punto cualquiera que forma parte de una función (Figura 5.10).

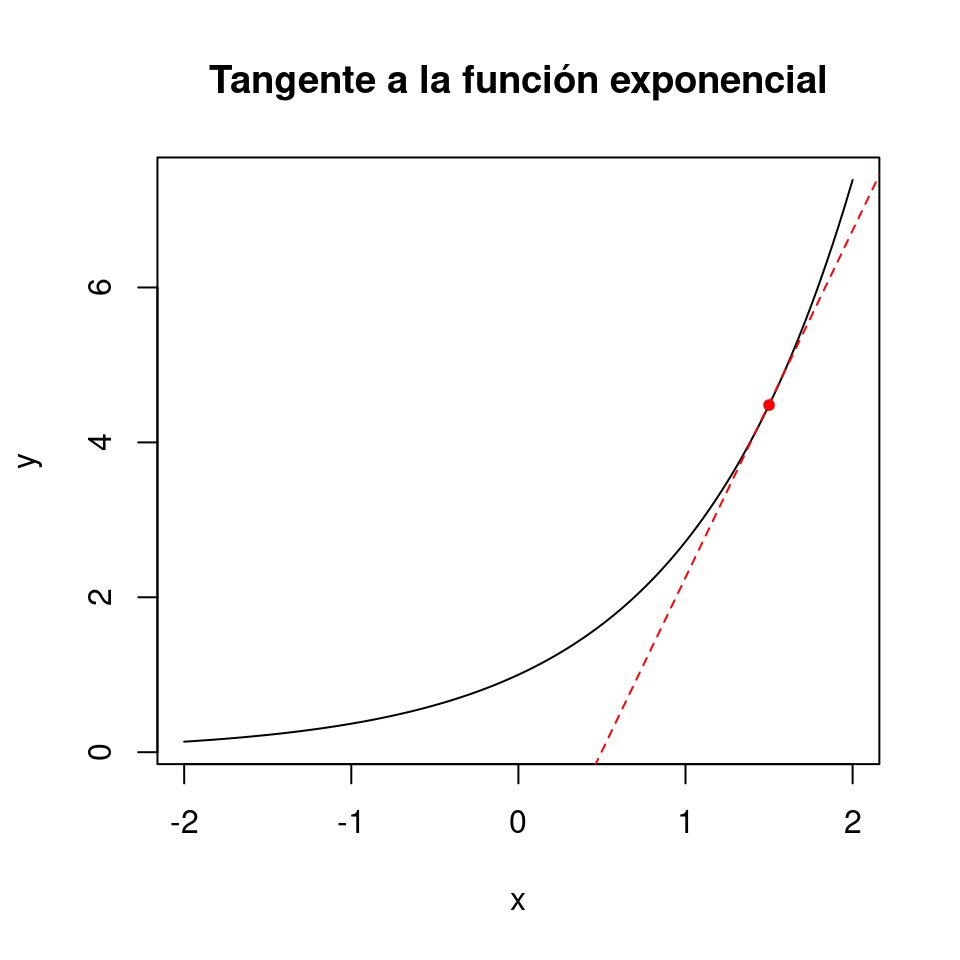
Figura 5.10: Representación gráfica de la tangente a un punto en la curva exponencial.

El proceso de estimar la pendiente de una tangente a la función en un punto \((x, f(x))\) consiste en estimar el límite:

\[\begin{equation} \lim \limits_{h \rightarrow 0} \frac{f(x + h) - f(x)}{x - (x + h)} \tag{5.6} \end{equation}\]

Resolverlo no requiere de un conocimiento profundo para encontrar que por sustitución directa de \(h = 0\), se obtiene una undeterminación (\(0/0\)). Sin embargo para entender mejor de qué se trata el límite de la ecuación (5.6) podemos explorarlo con la aplicación para derivadas.

5.3.1 Ejemplos

5.3.1.1 Ecuación cuadrática:

\[ y = x^2\] Con lo que la derivada sería:

\[\begin{equation} \lim \limits_{h \rightarrow 0} \frac{(x + h)^2 - x^2}{(x+h) - x} \end{equation}\]

Utilizando las técnicas para resolver límites podemos que con este último se puede utilizar factorización para obtener:

\[\begin{equation} \lim \limits_{h \rightarrow 0} \frac{(x + h)^2 - x^2}{(x+h) - x} = \lim \limits_{h \rightarrow 0} \frac{((x + h) - x)((x + h) - x)}{(x + h) + x} = \lim \limits_{h \rightarrow 0} (x + h) + x = \lim \limits_{h \rightarrow 0} 2x + h \end{equation}\]

Con este resultado podemos ahora sí sustituir \(h\) directamente para ver que la derivada \(y' = 2x\).

5.3.1.2 Hiperbola

\[ y = \frac{1}{x}\] Derivada:

\[\begin{equation} \lim \limits_{h \rightarrow 0} \frac{\frac{1}{x + h} - \frac{1}{x}}{(x+h) - x} \end{equation}\]

Podemos comenzar por simplificar las fracciones:

\[\begin{equation} \lim \limits_{h \rightarrow 0} \frac{\frac{x - (x + h)}{x(x + h)}}{h} = \lim \limits - \frac{h}{x^2 + xh} \frac{1}{h} = \lim \limits_{h \rightarrow 0} -\frac{1}{x^2} \end{equation}\]

Por lo tanto \(y' = \frac{1}{x^2}\)

5.3.2 Notación

La técnica de derivación se le atribuye a dos científicos, Isaac Newton y Gottfried Leibniz. La notación que se tradicionalmente enseña para comenzar con cáculo es la de Newton:

\[\begin{equation} f'(x) = \lim \limits_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \tag{5.7} \end{equation}\]

la cual adolece de claridad, pues a menos que uno conozca bien la fórmula de la derivada no especifica el significado de \(f'(x)\). La notación de Leibniz en cambio, sí lo especifica:

\[\begin{equation} \frac{df}{dx} = f'(x) \tag{5.8} \end{equation}\]

donde el numerador \(df = \Delta f = f(x + h) - f(x)\) y el denominador \(dx = \Delta x = (x+h) - x = h\). La letra \(d\) se utiliza en lugar de \(\Delta\) para indicar que se trata de un cambio contínuo, en lugar de discreto, el uso tradicional de \(\Delta\).

5.3.3 Reglas de derivación

5.3.3.1 Potencias

Como ya se habrán dado cuenta, la primera regla de la derivación está relacionada con los exponentes. Por ejemplo, la derivadas de \(f(x) = x^2\) y \(f(x) = \frac{1}{x}\), son \(\frac{df}{dx} = 2x\) y \(\frac{df}{dx} = - \frac{1}{x^2}\) respectivamente. Nota, que en ambos casos, los exponentes de cada \(x\), se convirtieron en coeficientes en \(\frac{df}{dx}\), y que restamos \(1\) a cada exponente de \(x\):

1. \(x^2 \rightarrow 2x^{2-1} = 2x^1 = 2x\)
2. \(1/x = x^{-1} \rightarrow -1x^{-1-1} = -x^{-2} = - 1/x^2\)

Entonces la primera regla de la derivación, se puede aplicar a muchas funciones. Si $f(x) = x^n $, $ = nx^{n-1} $.

En casos donde \(x\) aparece más de una vez, se considera que:

\[f(x) = f_1(x) + f_2{x} + \dots + f_n(x)\]

Y dado que la derivada es un límite, sabemos que \(f'(x) = f'_1(x) + f'_2(x) + \dots + f'_n(x)\).

Por ejemplo, si tenemos la función

\[y = a + bx + cx^2 + dx^3 = ax^0 + bx^1 + cx^2 + dx^3\]

su derivada será

\[ \frac{dy}{dx} = 0ax^{0-1} + bx^{1-1} + 2cx^{2-1} + 3dx^{3-1}= b + 2cx + 3dx^2\]

5.3.3.2 Productos

Si \(h(x) = f(x)g(x)\) entonces: \[h'(x) = f'(x)g(x) + f(x)g'(x)\]

5.3.3.3 Cocientes

Si \(h(x) = \frac{f(x)}{g(x)}\), entonces:

\[h'(x) = \frac{f'(x)g(x) - f(x)g'(x)}{g(x)^2}\]

5.3.3.4 Funciones en cadena

Una función en cadena es aquella en que \(h(x) = (f \circ g)(x) = f(g(x))\), entonces:

\[h'(x) = f'(g(x))g'(x) = (f \circ g)'(x) g'(x)\]

Aquí es preciso dar un ejemplo:

\[h(x) = (3x-1)^2\]

donde está claro que \(g(x) = 3x^2-1\) y que \(f(u) = u^2\). Por lo tanto si evaluamos \(f'(u)\) cuando \(u = 3x^2-1\), entonces \(f'(u) = 2(3x^2-1)\). Por el otro lado, tenemos que, aplicando la regla de las potnecias, \(g'(x) = 6x\). Entonces:

\[h'(x) = 2(3x^2-1)6x\]

5.3.4 Representación geométrica de la derivada

Como resultado del proceso de derivación de una función \(f(x)\) se obtiene una segunda función \(f'(x)\) ó \(\frac{d}{dx}f\) cufo valor corresponde a la pendiente de una tangente para cada par de valores \((x, f(x))\).

La aplicación Interpretación de la derivada, muestra ambas funciones y la recta tangente a \((x,f(x))\). Observa la pendiente de esta tangente y las coordenadas \((x, f'(x))\).

5.3.5 Aplicaciones

Uno de los modelos más generalizables que se utilizan en ecología es el de crecimiento exponencial:

\[N(t) = e^{rt}\]

Como vimos anteriormente, este modelo se puede linealizar utilizando el logaritmo:

\[\begin{equation} \ln N(t) = rt \tag{5.9} \end{equation}\]

y si resolvemos para \(r\), obtenemos que:

\[r = \frac{\ln N}{t}\]

la pendiente, o tasa de crecimiento de una poblaciones equivalente a \(\ln N/t\), para cualquier período de tiempo. Volvamos sin embargo a la ecuación (5.9), diferenciándola. Para esto utilizaremos la diferenciación implícita, pues necesitamos conocer:

1. \(\frac{d}{dt}rt = r\)
2. \(\frac{d}{dt}N(t) \ln N = \frac{d}{dt} \frac{1}{N}\)

por lo tanto:

\[\frac{dN}{dt} \frac{1}{N} = t\]

Con lo que obtenemos la siguiente ecuación diferencial:

\[\begin{equation} \frac{dN}{dt} = rN \end{equation}\]

De este modo podemos ver que, el crecimiento instantáneo de una población durante el intervalo \(dt\) es equivalente a la tasa de crecimiento exponencial \(r\). Más adelante veremos por qué \(f(x) = \ln x\), \(f'(x) = 1/x\), por el momento esta equivalencia nos sirve para ver que si \(N(t) = e^{rt}\):

\[\frac{dN}{dt} = e^{rt} = rN\] Y si separamos ambos lados \(N\) y \(t\), tenemos:

\[\frac{dN}{N} = r \cdot dt\]

Por lo tanto, la derivada nos sirve para estudiar de cerca la tasa de crecimiento en relación al cambio de población \(dN\) y de tiempo \(dt\), con un modelo lineal.

5.4 Integración

La integración es el proceso de estimación del área bajo la curva de una función, y para nosotros como ecólogxs es muyimportante, pues la mayoría de los modelos dinámicos se formulan como ecuaciones diferenciales, los cuales debemos integrar para obtener las soluciones.

Al igual que con límites y derivadas, hay toda una notación particular de la integración:

\[\begin{equation} \int_a^b \!f(x) dx \end{equation}\]

Y se lee, la integral de \(f(x)\) entre \(a\) y \(b\). \([a, b]\) corresponde a dos valores, mínimo (\(a\)) y máximo (\(b\)), de \(x\) entre los cuales se evaluará el área. El símbolo \(\int\), es una “S”, e indica la suma de valores contínuos. Al igual que en la derivada, el signo \(d\) es la versión contínua de \(\Delta\), en las integrales \(\int\) es la versión contínua de \(\sum\).

Otra similitud entre la dericada y la integral es que est última es un límite:

\[\begin{equation} \int_a^b \!f(x) dx = \lim \limits_{n \rightarrow \infty} \sum_{i = 1}^n f(x_i) \Delta x; \Delta x = \frac{b-a}{n} \tag{5.10} \end{equation}\]

Para comprederla, enfoquémonos en el lado derecho, que comenzando con el operador de sumatoria \(\sum\) indica que para cada valor \(x_i\), se evalúa la función \(f\), y se multiplica por la distancia que hay entre \(x_i\) y \(x_{i-1}\) (\(\Delta x\)). Si pensamos esto en el plano cartesiano, \(f(x_i)\) es la distancia entre \(0\) y el valor de \(y\) en \(f(x_i)\), por lo que al multiplicarlo por \(\Delta x\) estamos obteniendo el área de un rectángulo con lados de longitud \(\Delta x\) y \(f(x_i)\). Nota que conforme \(n \rightarrow \infty\), la longiud de \(\Delta x\) disminuye tanto, que el número de rectángulos con área \(\Delta x \times f(x_i)\) tiende a infinito.

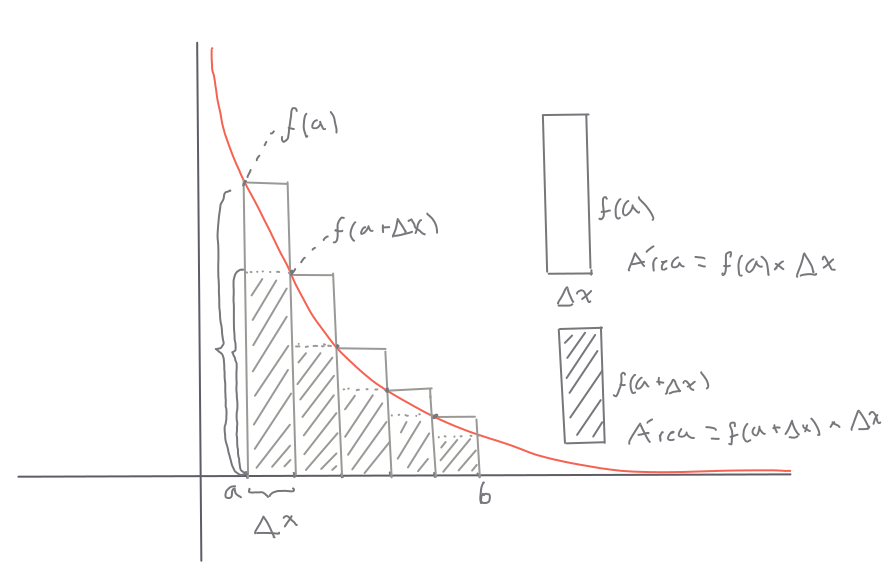
Figura 5.11: Representación esquemática de la integral. Nota quq utilizando los rectángulos, es posible aproximar el valor de una integral con rectángulos que pasen por arriba o abajo de la curva.

Puedes explorar estos conceptos con la aplicación para el área bajo una recta de Geogebra.

5.4.1 Área bajo una recta

Un ejemplo clásico de integración es el área bajo una recta con pendiente \(m \neq 0\) e intercepto \(0\), la cual corresponde al área de un triángulo (figura 5.12).

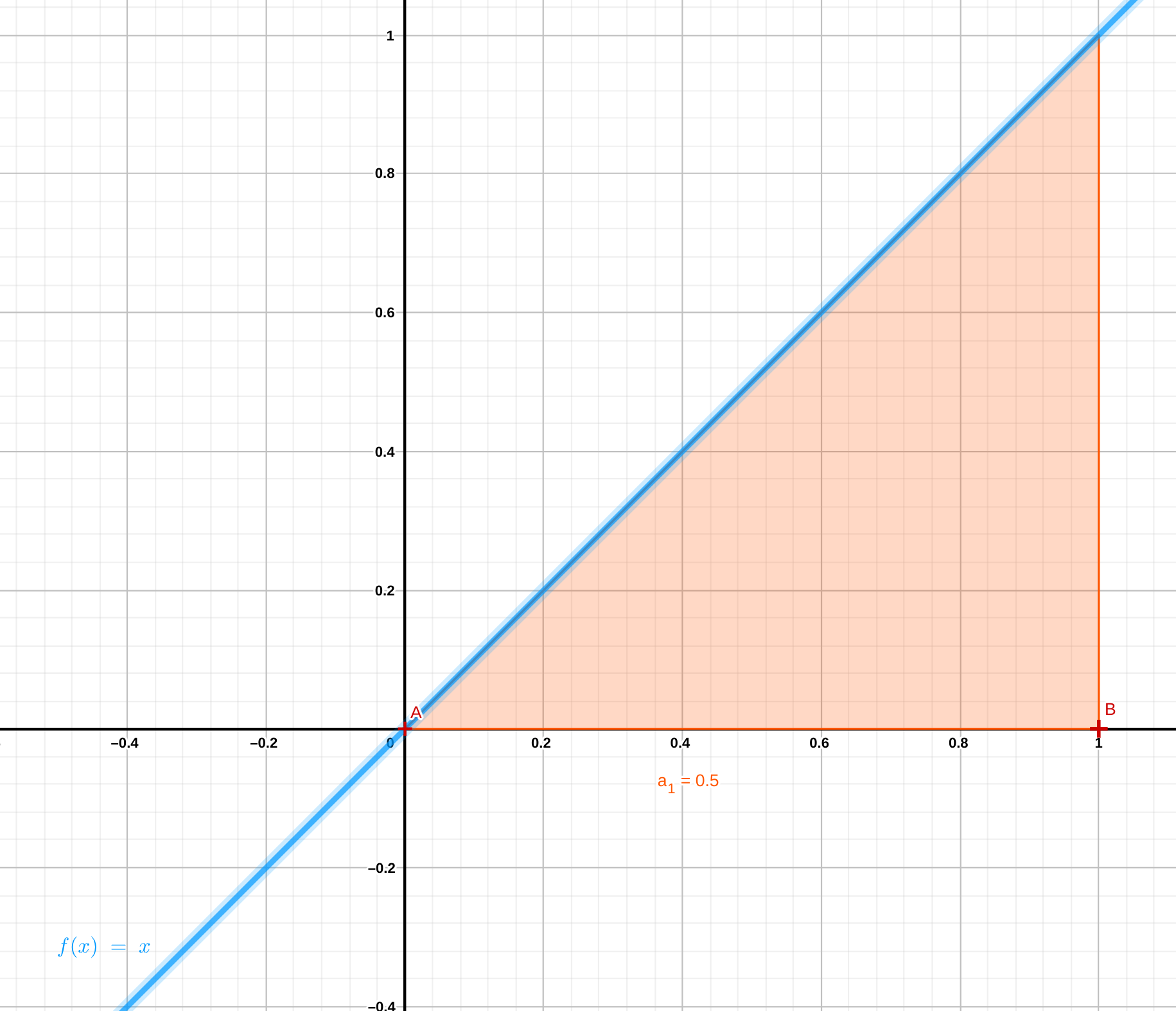
Figura 5.12: Área bajo la recta f(x) = x, entre el punto 0 y a = 1.

Utilizando el método de los rectángulos tenemos que el área sombreada en la figura 5.12 entre los puntos \(0\) y \(a\) se puede aproximar sumando rectángulos con altura \(f(x)\) y ancho \(\Delta x\).

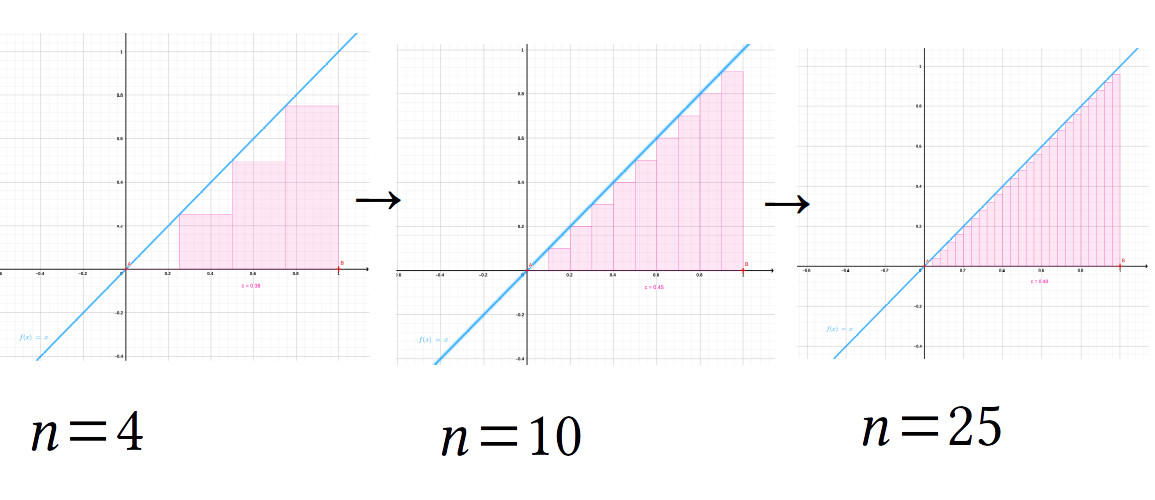
Figura 5.13: Método de los rectángulos para calcular área bajo curva

Para automatizar este proceso y encontrar todos los valores de \(x\) en el intervalo \(0, a\), podemos comenzar por tomar en cuenta el número de rectángulos, como en la figura 5.13, cuantos más rectángulos tenemos el error de cálculo será menor.

La siguiente consideración será si tomaremos en cuenta el punto inferior o superior del intervalo (figura 5.11). Si tomamos en cuenta el punto inferior del intervalo, la altura del primer rectángulo será \(f(0)\), y el ancho será \(\Delta x = a/n\). Por otra parte, tenemos que los valores de \(x\) en que evaluaremos \(f(x)\) corresponden a los valores de \(x: 0, a/n, 2a/n, 3a/n, \dots, (n-1)a/n, a\), Si comenzamos con \(n = 10\), y \(a = 1\) tenemos que evaluar \(f(x)\) en los valores:

\[x = \left \{ 0, \frac{1}{10}, \frac{1}{10}, \dots, \frac{9}{10}, 1 \right \}\]

Estas integrales se comoces como de Riemann. Por muchos años los matemáticos se dieron a la tarea de encontrar las funciones que resultaban de incremetar el número de rectángulos bajo la curva de diversas funciones. No fue sino hasta que Newton y Leibniz acuñaron el teorema fundamental del cálculo que se obtuvieron las herramientas necesarias para estimar fácilmente el ára bajo la curva de cualquier función.

De aquí en adelante está en construcción, no usar!

5.4.2 El teorema funamental del cálculo

Este teorema establece, en términos muy generales que

\[\begin{equation} \int \frac{d}{dx}f = f(x) \end{equation}\]

la integral de una derivada es la función misma con la que se obtuvo la derivada. Así, llegamos a la antiderivada.

5.4.2.1 Antiderivadas de funciones

Bajo la regla de las potencias, que si \(f(x) = ax^n\), \(\int f(x) = \frac{ax^{n+1}}{n+1}\). Si derivamos \(\int f(x)\), veremos que \(f(x) = ax^n\).

Esta sencillísima técnica es efectiva para funciones sin constantes, puesto que la derivada de una constante es 0. Sin embargo debido a que al integrar una función no tenemos ningún conocimiento sobre la existencia o ausencia de una constante (p. ej. \(y = a + bx\)), es necesario asumir su existencia, de modo que:

\[\begin{equation} \int f(x) = \frac{ax^{n+1}}{n+1} + c \end{equation}\]

donde \(c\) es la constante de integración.

5.4.3 Aplicaciones de la integración

5.4.3.1 Cambio acumulativo

El modelo de crecimiento exponencial, basado en la ecuación:

\[\begin{equation} N(t) = e^{rt} \tag{5.11} \end{equation}\]

es la base de un gran número de modelos en ecología. Cuando transformamos este modelo en una ecuación diferencial, toma una apariencia un tanto diferente. Comencemos por recordar que si \(f(x) = e^x\), entonces \(f'(x) = e^x\). Si agregamos un parámetro \(r\) como coeficiente de \(x\), tenemos que \(f(x)= e^{rx}\), resultando exactamente en el modelo (5.11).

Para derivar este modelo necesitamos recordar que:

\[\frac{d}{dx}(f \circ g)(x) = (f \circ g)'(x)g'(x)\] y por analogía \((f \circ g)(x) = e^{rt}\) y \(g(x) = rt\), por lo tanto:

\[\begin{equation} \frac{dN}{dt} = r e^{rt} \end{equation}\]

donde podemos sustituir \(e^{rt}\) por \(N\), para obtener:

\[\begin{equation} \frac{dN}{dt} = r N \end{equation}\]

que el cambio inmediato en el número de individuos de la población \(N\), es proporcional a \(rN\). La integral \(\int_{0}^{t} \frac{dN}{dt}\) es entonces equivalente al número de individuos en ese momento \(t\), mientras que \(\int_{0}^{t} N(t)\) corresponde al número total de individuos que hay y ha habido en esa población!

5.4.3.2 Integración analítica vs numérica

En matemáticas, el término analítico se utiliza para describir el proceso de encontrar con herramientas formales de las matemáticas una solución exacta a un problema. Por ejemplo la antiderivación, aplicando a la inversa las relgas de la derivación es la integración analítica. Hay modelos sin embargo que no se pueden resolver con herramientas analíticas, típicamente, aquellos en que no podemos separar las variables dependientes e independientes. En esos casos hacemos integración numérica, que consiste en aproximaciones al valor de la función pero nunca representan las soluciones exactas que se obtienen con integración analítica.

Veamos la ecuación diferencial:

\[\begin{equation} \frac{dN}{dt} = rN \tag{5.12} \end{equation}\]

corresponde a una función que conocemos como \(N = e^{rt}\), sin embargo podríamos aproximarnos recursivamente a los valores que prediciría \(e^{rt}\) utilizando la definición de la derivada. Sabemos que la derivada es la pendiente de una recta, por lo tanto podríamos comenzar por dibujar una recta con pendiente \(rN\) partiendo desde \(t = 0\), hasta un punto \(0+dx\). El cambio absoluto de \(N\) (\(dN\)) sería entonces \(rN \times dt\), cuyo valorr utilizaremos como punto de partida. Mencioné anteriormente que este método es una aproximación, y esto es porque resulta en un error que se va acumulando entre la función verdadera \(N = e^{rt}\) y la que aproximamos revirtiendo secuencialmente la derivada (figura ).

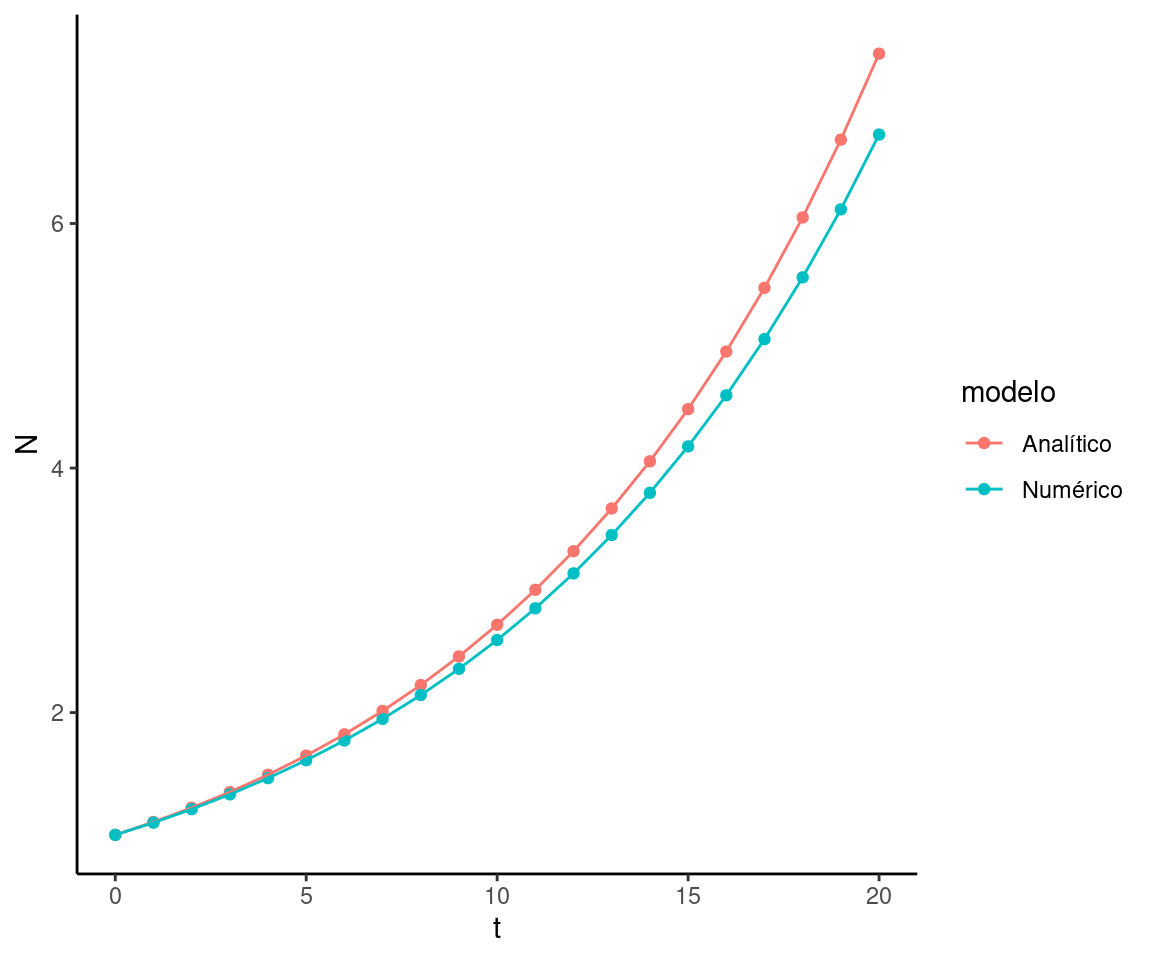
Figura 5.14: Diferencias entre integración analítica vs integración numérica, para r = 0.1, dt = 1, y población inicial de N = 1.